1. Оптимальный выбор БСК в одном узле по критерию минимума
приведённых затрат, на установку БСК и дальнейшую эксплуатацию сети.
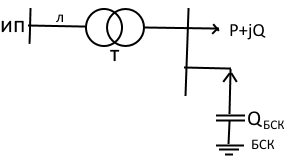
Затраты равны:
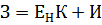
Где 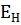 – коэффициент сравнительной эффективности капиталовложений
– коэффициент сравнительной эффективности капиталовложений 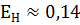
К – капиталовложения в установку БСК, будем их считать прямо пропорциональными мощности БСК.
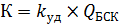
Где 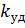 – коэффициент пропорциональности
– коэффициент пропорциональности
И – годовые эксплуатационные издержки
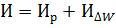
Где 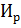 – издержки на ремонт и обслуживание БСК, будем их считать независящими от мощности БСК.
– издержки на ремонт и обслуживание БСК, будем их считать независящими от мощности БСК.
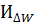 – годовая стоимость потерь электроэнергии. Будем здесь учитывать только потери на передачу реактивной мощности в линии и трансформаторе, и потери в самой БСК, тогда:
– годовая стоимость потерь электроэнергии. Будем здесь учитывать только потери на передачу реактивной мощности в линии и трансформаторе, и потери в самой БСК, тогда:
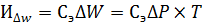
Где 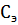 – стоимость электроэнергии,
– стоимость электроэнергии, 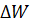 – потери энергии за год,
– потери энергии за год, 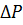 – потери активной мощности,
– потери активной мощности, 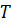 – время переводящее потери мощности, потери энергии.
– время переводящее потери мощности, потери энергии.
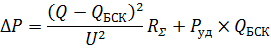
Где 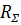 – суммарное сопротивление линии и трансформатора,
– суммарное сопротивление линии и трансформатора, 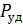 – удельная потеря мощности в БСК.
– удельная потеря мощности в БСК.
Поскольку издержки на ремонт и обслуживание постоянны, то исключим их из целевой функции, тогда сводя все формулы в одну, получим:
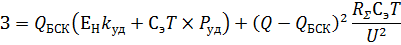
Найдём минимум затрат классическим способом:
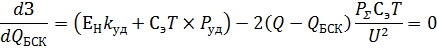
Отсюда находим:
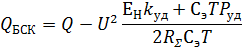
2. Оптимизация размещения БСК в радиальной сети.
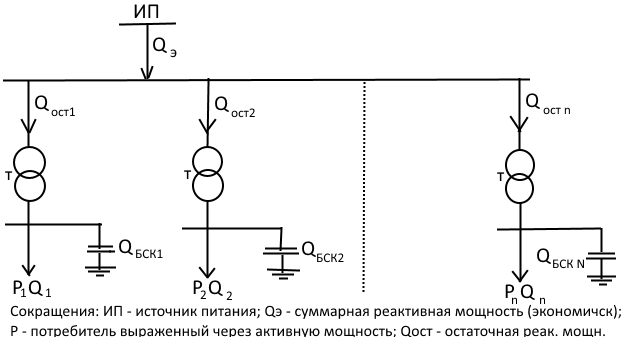
Задана суммарная реактивная мощность 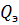 , которая должна потребляться при условии компенсации. Тогда ограничение равенства имеет вид:
, которая должна потребляться при условии компенсации. Тогда ограничение равенства имеет вид:
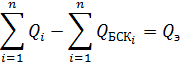
Отсюда видно, что суммарная мощность БСК это постоянная величина, поэтому задача сводится к распределению этой мощности между узлами. Капиталовложения тоже будут постоянной величиной, поэтому их можно исключить из целевой функции и перейти от минимизации затрат к минимизации потерь активной мощности, причём потери в самих БСК тоже можно не учитывать, поскольку их суммарная величина постоянна. Тогда целевой функцией будут суммарные потери на передачу реактивной мощности в сети:
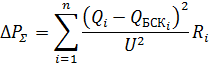
Где 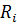 – сопротивление линии и трансформатора i – той ветви.
– сопротивление линии и трансформатора i – той ветви.
Из целевой функции можно исключить напряжение как постоянный коэффициент. Заменим на 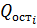 выражение
выражение 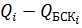 , тогда целевая функция примет вид:
, тогда целевая функция примет вид:
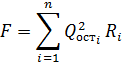
Техническое ограничение запишется в виде:
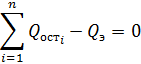
Используем метод Лагранжа:
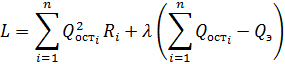
Найдём минимум этой функции:
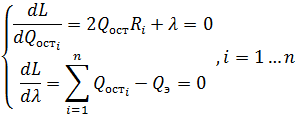
Из первого уравнения следует, что:
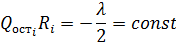
То есть
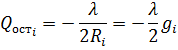
Где 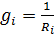 (проводимость)
(проводимость)
Тогда из второго уравнения мы будем иметь:
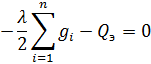
Отсюда:
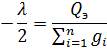
Тогда:
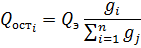
И в итоге:
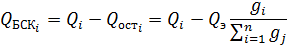
 2015-04-06
2015-04-06 1202
1202