Пусть имеется функция 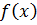 , требуется найти оптимальное значение
, требуется найти оптимальное значение 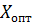 , при котором f имеет минимум. Условие экстремума это равенство нулю первой производной функции
, при котором f имеет минимум. Условие экстремума это равенство нулю первой производной функции 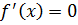 , это условие представляет собой алгебраическое уравнение. Необходимо найти все его действительные корни (
, это условие представляет собой алгебраическое уравнение. Необходимо найти все его действительные корни (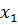 ,
, 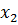 … и т. д.). После этого вычисляются все значения функции
… и т. д.). После этого вычисляются все значения функции 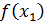 ,
, 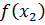 , и т. д. Определяется минимальное из этих значений (путём сравнения), тогда значение x, при котором функция минимальна и является решением этой задачи т. е.
, и т. д. Определяется минимальное из этих значений (путём сравнения), тогда значение x, при котором функция минимальна и является решением этой задачи т. е. 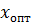 .
.
Классическая минимизация функции одной переменной
|
|

Сейчас читают про:
 2015-04-06
2015-04-06 728
728







