Задачи к разделу 3

3.1. Сообщения источника, имеющего алфавит объемом 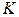, кодируется двоичным блочным кодом (табл. 3.1). Количество разрядов в каждой кодовой комбинации 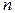. Какое число информационных и проверочных символов содержится в каждой кодовой комбинации? Сколько разрешенных и запрещенных комбинаций в используемом коде? Определить избыточность и относительную скорость кода.

Таблица 3.1

Вариант	а)	б)	в)	г)	д)	е)	ж)	з)	и)	к)

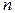3.2. Определить минимальное кодовое расстояние 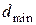для кодов обнаруживающих 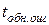ошибок и исправляющих 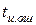ошибок (табл. 3.2).

Таблица 3.2

Вариант	а)	б)	в)	г)	д)	е)	ж)	з)	и)	к)

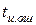3.3. Двоичный код, предназначенный для кодирования 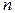сообщений, содержит кодовые комбинации (табл. 3.3).

Таблица 3.3

Вариант	а)	б)	в)	г)	д)

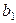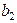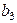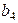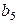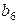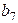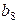Является ли данный код линейным? Найти избыточность и относительную скорость кода.

3.4. Построить порождающую матрицу для кода с минимальным кодовым расстоянием 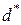, количеством информационных элементов 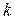(табл. 3.4). Написать правила формирования проверочных элементов для полученного кода. Найти проверочную матрицу. Определить, сколько ошибок такой код может обнаружить и исправить. Нарисовать структурные схемы кодирующего и декодирующего устройства. Составить таблицу соответствия между местоположением одиночных ошибок и видом синдрома.

Таблица 3.4

Вариант	а)	б)	в)	г)	д)	е)	ж)	з)	и)	к)

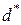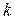3.5. Найти порождающую матрицу для кода с минимальным кодовым расстоянием 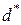, количеством разрядов в кодовой комбинации 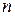(табл. 3.5). Построить проверочную матрицу. Определить, сколько ошибок будет исправлять и обнаруживать код, а также скорость передачи.

Таблица 3.5

Вариант	а)	б)	в)	г)	д)	е)	ж)	з)	и)	к)

3.6. Код построен по матрице

.

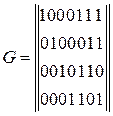Определить, какие из приведенных кодовых комбинаций линейного кода содержат ошибку (табл. 3.6).

Таблица 3.6

Вариант	а)	б)	в)	г)	д)

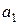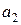3.7. Порождающая матрица (n,k)-кода над 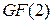имеет вид

.

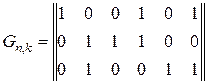Необходимо:

а) найти порождающую и поверочную матрицы эквивалентного систематического кода;

б) найти кодовое слово, соответствующее информационной последовательности 101;

в) декодировать принятое слово 111100.

3.8. Найти 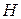, 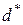для линейного блокового кода, изобразить схему кодера и декодера, если порождающая матрица блочного кода имеет вид

а) ;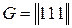

б) ;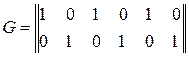

в) ;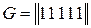

г) .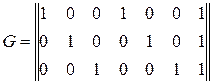

3.9. Найти порождающую матрицу кода, построить схемы кодирующего и декодирующего устройств, найти 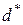кода, определить возможности кода по обнаружению и исправлению ошибок, если проверочная матрица имеет вид

а) ;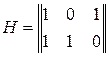

б) ;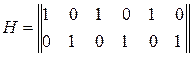

в) ;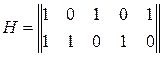

г) .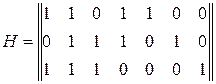

3.10. Схема кодера линейного блочного кода приведена на рис. 3.1. Найти 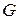, , 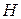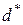. Изобразить схему синдромного декодера.

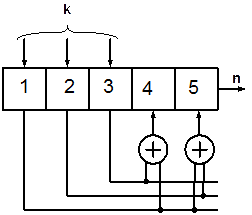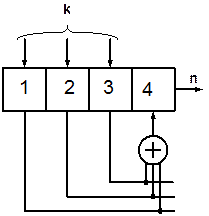а)	б)
Рис.3.1

3.11. Для разделимого и неразделимого циклических кодов (7, 4) с порождающим полиномом 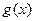=1011 и кодовой комбинацией простого кода 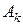=0101 определить:

а) кодовые комбинации;

б) схемы кодеров и декодеров;

в) порождающие и проверочные матрицы.

3.12. Решить задачу 3.11 для кода (15, 11) с порождающим полиномом 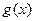=10011 и информационными символами 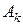=11111000001.

3.13. Многочлен g(x)=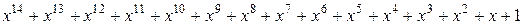

порождает циклический код над GF(2) длины 15.

Необходимо:

а) найти проверочную матрицу кода;

б) определить число ошибок, которое может исправить код;

3.14. Найти ошибочные разряды в кодовых словах циклического кода, порождающий многочлен которого имеет вид g(x)=x⁸+x⁷+ x⁶+x⁴+1:

а) 101100101011010	(3 ошибки);
б) 111000101101010	(1 ошибка);
в) 100101001011010	(2 ошибки);
г) 111101001101010	(2 ошибки).

3.15. Определить ошибочно принятый элемент в кодовой комбинации:

а) 10111111100, если порождающий полином ;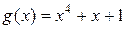

б) 1000110, если порождающий полином .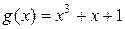

3.16. Можно ли с помощью порождающего многочлена 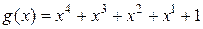исправить все одиночные ошибки в циклическом коде (15, 11)? Получить проверочный многочлен данного кода.

3.17. Дана четырехразрядная кодовая комбинация простого кода 1011. Построить циклический код на базе порождающего полинома .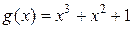

3.18. Сверточный код описывается полиномами , , .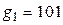

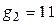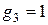Необходимо:

а) получить кодер, соответствующий этому коду;

б) построить диаграмму состояний для этого кода;

в) определить последовательность на выходе кодера, если на вход поступают символы 11001;

г) декодировать последовательность 111000000000.

3.19. Задачу 3.18 решить для сверточных кодов, заданных полиномами:

а) , , ;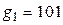

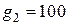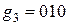б) , ;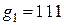

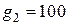в) , .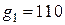

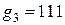3.20. Нарисуйте схему кодера по следующим параметрам: скорость кода 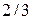, , 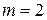свободное расстояние 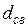=5. Получить диаграмму состояний для данного кодера. Определить последовательность на выходе кодера, если на вход поступают символы: 11001. Определить число исправляющих ошибок 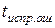, длину кодового ограничения .

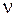3.21. Построить схему кодера по следующим параметрам:

а) скорость кода 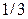, , 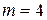свободное расстояние 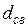=5;

б) скорость кода 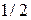, , 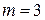свободное расстояние 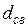=5;

в) скорость кода 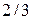, , 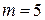свободное расстояние 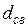=7.

3.22. Для сверточного кода, генерируемого кодером (рис. 3.2 - 3.6), определить: порождающие полиномы; характеристики кода: , , , , , , , ,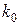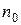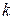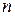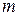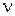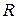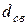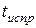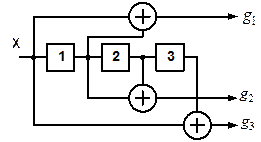
	а)
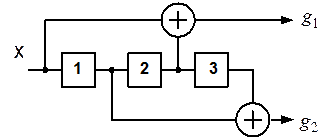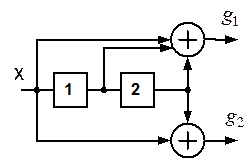б)	в)
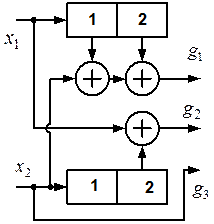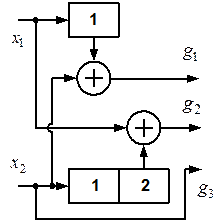г)	д)