Сверточные коды характеризуются следующими параметрами:
- длиной кодового ограничения
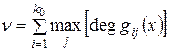 ,
,
где 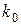 - входной кадр поступающих символов;
- входной кадр поступающих символов;
deg - функция, определяющая максимальную степень полинома;
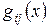 - порождающие полиномы;
- порождающие полиномы;
- информационной длиной кодового слова
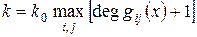 ;
;
- кодовой длиной блока
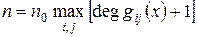 ,
,
где 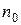 - выходной кадр символов;
- выходной кадр символов;
- свободным кодовым расстоянием 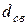 , которое определяется как суммарное количество единиц в порождающих полиномах.
, которое определяется как суммарное количество единиц в порождающих полиномах.
Сверточный код требует для своего описания нескольких порождающих многочленов – в общем случае 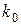
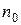 . Порождающие многочлены могут быть объединены в порождающую матрицу
. Порождающие многочлены могут быть объединены в порождающую матрицу 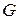 :
:
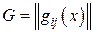 . . | (3.14) |
Операцию кодирования можно описать с помощью векторно-матричного произведения
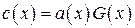 , , | (3.15) |
или
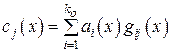 , , | (3.16) |
где 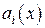 - информационные символы.
- информационные символы.
Проверочная матрица 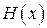 из многочленов является
из многочленов является 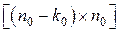 - матрицей, элементами которой являются многочлены и которая удовлетворяет условию
- матрицей, элементами которой являются многочлены и которая удовлетворяет условию
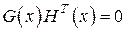 . . | (3.17) |
Вектор синдромных многочленов определяется выражением
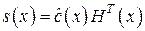 . . | (3.18) |
Для систематического сверточного кода (например, для кода Вайнера-Эша) порождающая 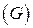 и проверочная матрицы
и проверочная матрицы 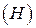 имеют вид
имеют вид
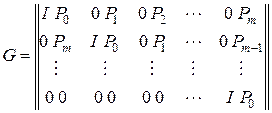 , , | (3.19) |
где 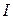 - единичная матрица
- единичная матрица 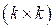 ;
;
0 – матрица, состоящая из нулей 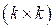 ;
;
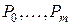 - матрица размерами
- матрица размерами 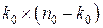 ;
;
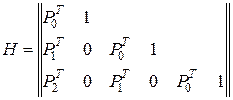 , , | (3.20) |
где 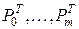 - транспонированные матрицы
- транспонированные матрицы 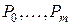 .
.
 2015-04-06
2015-04-06 1071
1071








