2015-04-06
832
Двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в форме основной задачи, для которой среди векторов Рj составленных из коэффициентов при неизвестных в системе уравнений, имеется т единичных. Вместе с тем двойственный симплекс-метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Такую задачу и рассмотрим теперь, предварительно предположив, что единичными являются векторы P1, Р2,..., Рт, т. е. рассмотрим задачу, состоящую в определении максимального значения функции
F= с1х1 + с2х2 +…+ спхп (1)
при условиях
x1P1+ x2P2+…+ xmPm+ xm+1Pm+1+…+ x1P1=P0 , (2)
xj≥0 (j=1,n), (3)
где Р1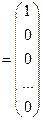 
; Р2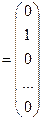 
; …; Рm 
;
= 
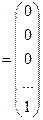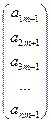; …; Рn= 
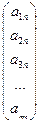; Р0=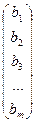 
и Рm среди чисел bi, (i=1,m) имеются отрицательные.
В данном случае Х=(b1;b2;...; bт; 0;...;0) есть решение системы линейных уравнений (1). Однако это решение не является планом задачи, так как среди его компонент имеются отрицательные числа.
|
|
|
Поскольку ректоры Р1, Р2,...,Рт — единичные, каждый из векторов Pj (j=1,n) можно представить в виде линейной комбинации данных векторов, причем коэффициентами разложения векторов Pj по векторам
P1, Р2,..., Рт служат числа хij=aij (i=1,m; j=1,n). Таким образом, можно m
∆j =zj-cj=∑ ciaij-сj (j=1,n).
i=1
Решение Х=(b1;b2;...; bт; 0;...;0) системы линейных уравнений (1), определяемое базисом Р1, Р2,...,Рт, называется п севд опланом задачи (1) — (3), если ∆j≥0 для любого j (j=1,n).
Теорема 1. Если в псевдоплане Х=(b1;b2;...; bт; 0;...;0), определяемом базисом Р1, Р2,...,Рт, есть хотя бы_одно отрицательное число bi<0 такое, что все aij ≥ 0 (j=1,n),то задача (1) — (3) вообще не имеет планов.
Теорема 2. Если в псевдоплане Х=(b1;b2;...; bт; 0;...;0), определяемом базисом Р1, Р2,...,Рт имеются отрицательные числа bi<0 такие, что для любого из них существуют числа aij <0, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (1) — (3) не уменьшится.
Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.
Таким образом, отыскание решения задачи (1) — (3) двойственным симплекс-методом включает следующие этапы:
1. Находят псевдоплан задачи.
2. Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.
3. Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца вектора Ро и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов (m+l)-й строки к соответствующим отрицательным элементам разрешающей строки.
|
|
|
4. Находят новый псевдоплан и повторяют все действия, начиная с этапа 2.
Таблица 2
| i | Базис | Cб | P0 | C1 | C2 | … | Ce | … | Cm | Cm+1 | … | Cr | … | Cn |
| P1 | P2 | … | Pe | … | Pm | Pm+1 | … | Pr | … | Pn | ||||
| P1 | C1 | b1 | … | … | a1m+1 | … | a1r | … | a1n | |||||
| P2 | C2 | b2 | … | … | a2m+1 | … | a2r | … | a2n | |||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| e | Pe | Pe | be | … | … | aem+1 | … | aer | … | aen | ||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| i | Pi | Ci | bi | … | … | aim+1 | … | air | … | ain | ||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | ... |
| m | Pm | Cm | bm | … | … | amm+1 | … | amr | … | amn | ||||
| m+1 | F0 | … | … | Δm+1 | … | Δr | … | Δn |
Контрольные вопросы
- Перечислить этапы алгоритма двойственного симплексного метода.
- Каким образом можно судить об оптимальности полученного решения?
- Когда задача не имеет решения?
- Как определяется разрешающая строка?
- Как определяется разрешающий столбец?
- Дать сравнительную характеристику симплексного метода и двойственного симплексного метода.
