Формула Эйлера:
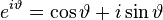
позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
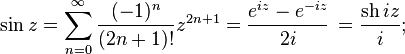
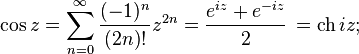
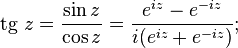
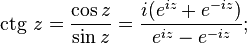
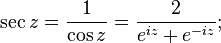
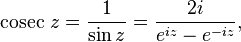 где
где 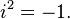
Соответственно, для вещественного x,
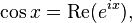
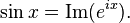
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
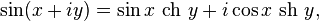
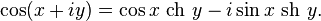
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Функция: y=x\n – ее свойства и график.
| Рассмотрим функцию, заданную формулой y = xn, где х – независимая переменная, а n – натуральное число. Такую функцию называют степенной функцией с натуральным показателем. Степенные функции при n =1, 2 и 3, т. е. функции y = x 1, y = x 2 и y = x 3, уже рассматривались в нашем курсе. Их свойства и графики нам известны. Выясним теперь свойства степенной функции и особенности её графика при любом натуральном n. Выражение xn, где n – натуральное число, имеет смысл при любом х. Поэтому областью определения степенной функции с натуральным показателем является множество всех действительных чисел. Сначала рассмотрим случай, когда показатель n – чётное число. Свойства функции y = xn при чётном n аналогичны свойствам функции y = x 2. |
| 1. Если х =0, то у =0. График функции проходит через начало координат. 2. Если х 0, то y >0. Это следует из того, что чётная степень как положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях. 3. Функцияявляется чётной. Это следует из того, что при чётном n равенство (– x) n = xn верно для любого x. График функции симметричен относительно оси ординат. 4. Функция возрастаетв промежутке [0; +) иубываетв промежутке (–; 0]. |
| Рис. 1 | Действительно, пусть x 2 > x 1 0. Если x 1=0, то очевидно, что. Если x 1>0, то перемножив почленно n одинаковых неравенств x 2> x 1, получим верное неравенство. Значит, в промежутке [0; +) функция возрастает. Пусть теперь x 1 и x 2 принадлежат промежутку (–; 0] и x 2< x 10. Тогда –x 2>– x 1 0 и по доказанному выше (–x 2) n >(– x 1) n. Отсюда в силу чётности n следует, что. Значит, в промежутке (–; 0] функция убывает. С возрастанием х график функции слева от начала координат опускается вниз, а справа поднимается вверх. На рисунке 1 изображены графики функций y = x 2 и y = x 4. |
| 5. Область значений функции есть множество неотрицательных чисел. |
| Рассмотрим теперь свойства степенной функции y = xn, когда показатель n – нечётное число. |
| 1. Если х =0, то у =0. График функции проходит через начало координат. 2. Если х >0, то y >0, если то х <0, то y <0. График функции расположен в первой и третьей координатных четвертях. 3. Функция является нечётной. Это следует из того, что при нечётном n для любого х верно равенство (– x) n =– xn. График функции симметричен относительно начала координат. 4. Функция возрастаетна всей области определения. |
| Доказательство того, что функция возрастает в промежутке [0; +) проводится так же, как и для степенной функции с чётным показателем. Докажем, что функция возрастает также в промежутке (–; 0]. Пусть x 1 и x 2 принадлежат этому промежутку и x 2> x 1. Тогда 0 –x 2<– x 1. Так как –x 20 и –x 10, то (–x 2) n <(– x 1) n. В силу нечётности числа n заключаем, что. Значит, функция возрастает и в промежутке (–; 0]. Если же x 1<0, а x 2>0, то очевидно, что. Значит, функция возрастает на всей области определения. График функции с возрастанием х поднимается вверх. |
| 5. Область значений функции есть множество всех действительных чисел. |
| Это следует из свойств 1–3 и из того, что любое неотрицательное число является значением степенной функции с неотрицательным показателем при некотором x 0. График функции пересекает любая прямая y = a. На рисунке 2 изображены графики функций y = x 3 и y = x 5. | ||||||||||||||||
|
 2015-04-06
2015-04-06 670
670







