Дифференциалы высших порядков

Производные и дифференциалы высших порядков.

Производные и дифференциалы высших порядков

Пусть в интервале (a, b) задана функция f (x) и в каждой точке x Î (a, b) существует производная f '(x). Таким образом в интервале (a, b) задана функция y = f '(x).

Если первая производная функция y = f '(x) дифференцируема в интервале (a, b), то ее производная называется второй производной функции f (x).

Вторая производная обозначается символами f ''(x) или

d ² f

dx ²

Вообще, производной n–го порядка функции f (x), называется производная от производной функции f (x) (n − 1)–го порядка. Производная n –го порядка обозначается f ⁽ⁿ⁾ (x).

Замечание. Если речь идет о производной n –го порядка (n = 2, 3, …) в фиксированной точке x ₀, то для существования f ⁽ⁿ⁾ (x ₀) необходимо существование f ^{(n − 1)} (x) не только в точке x ₀, но и в некоторой ее окрестности. При этом условии

f ⁽ⁿ⁾ (x ₀) =

f ^{(n − 1)} (x ₀).

Функция, имеющая в точке производную n –го порядка, называется n раз дифференцируемой в этой точке.

Функция, имеющая в точке производные всех порядков, называется бесконечно дифференцируемой в этой точке.

Формулы для производных n –го порядка суммы и произведения функций

Если функции u (x) и v (x) n раз дифференцируемы на некотором промежутке, то производная n –го порядка суммы определяется формулой

(u + v)⁽ⁿ⁾ = u ⁽ⁿ⁾ + v ⁽ⁿ⁾,

а производная n –го порядка произведения определяется формулой Лейбница

(u · v)⁽ⁿ⁾ = u ⁽ⁿ⁾ · v + n u ^{(n − 1)} · v ' +

n (n − 1)

2!

u ^{(n − 2)} · v '' + … + u · v ⁽ⁿ⁾.

Формула Лейбница может быть записана в виде

(u · v)⁽ⁿ⁾ =

n

∑

k = 0

C_n^k · u ^{(n − k)} v ^(k),

где u ⁽⁰⁾ = u (x), v ⁽⁰⁾ = v (x) и C_n^k =

n!

k! (n − k)!

— биномиальные коэффициенты.

Дифференциалы высших порядков

Пусть в интервале (a, b) задана дважды дифференцируемая функция y = f (x), где x — независимая переменная.

Фиксируем приращение dx = Δ x независимой переменной x, т.е. будем считать первый дифференциал

dy = f '(x) dx

(1)

функцией только переменной x.

Дифференциал от первого дифференциала, при условии, что повторное приращение независимой переменной x совпадает с первоначальным, называется вторым дифференциалом функции f (x) в точке x и обозначается d ² f (x).

Дифференцируем выражение в правой части (1) как произведение

d ² f (x) = d (df (x)) = d (f '(x) dx) = f ''(x) dx · dx + f '(x) · d (dx).

Учитывая, что d (dx) = 0, получаем формулу для вычисления второго дифференциала

d ² f (x) = f ''(x) dx ².

(2)

Пусть в интервале (a, b) функция f (x) имеет производные до n –го порядка включительно.

Дифференциалом n –го порядка называется дифференциал от дифференциала (n − 1)–го порядка

dⁿ f (x) = d (d ^{(n − 1)} f (x)).

Формула для вычисления дифференциала n–го порядка

dⁿ f (x) = f ⁽ⁿ⁾ (x) dxⁿ.

Неинвариантность формы дифференциала порядка выше первого

Рассмотрим случай, когда х является не независимой переменной, а функцией от другой переменной

y = f (x), x = j (u).

В силу инвариантности формы первого дифференциала имеем

dy = f '(x) dx.

(3)

Теперь в правой части формулы (3) от переменной u зависит не только функция f (x), но и дифференциал dx. Следовательно

dx = j '(u) du, d ² x = j ''(u) du ².

Таким образом, в общем случае

d ² y = f ''(x) dx ² + f '(x) d ² x.

(4)

Сравнивая формулы (2) и (4), убеждаемся, что дифференциалы второго (и более высоких порядков) не обладают инвариантностью формы.

41. Правило Лопиталя для раскрытия неопределенностей вида 0/0, ∞/∞.

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 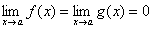или 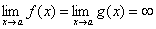. Тогда, если существует предел отношения производных этих функций 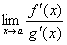, то существует и предел отношения самих функций f(x)/g(x) при x → а, причем

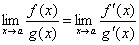(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти 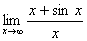. Этот предел существует 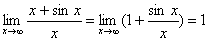. Но отношение производных ( 1 + cos x)/ 1 = 1 + cos x при x →∞ не стремится ни к какому пределу.

Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.

Для раскрытия неопределенностей 1^∞, 1⁰, ∞⁰ нужно прологарифмировать данную функцию и найти предел ее логарифма.

42. Экстремумы функции y=f(x). Необходимое и достаточное условия существования экстремума. Критические точки.

Локальные экстремумы функции

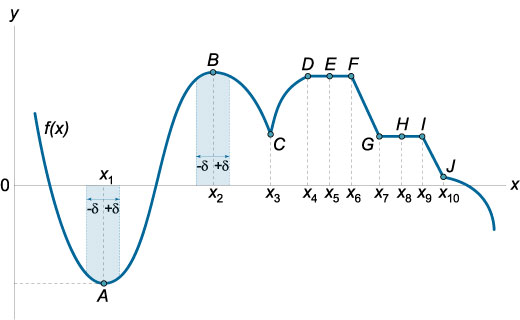
Определение локального максимума и локального минимума Пусть функция y = f (x) определена в некоторой δ -окрестности точки x ₀, где δ > 0. Говорят, что функция f (x) имеет локальный максимум в точке x ₀, если для всех точек x ≠ x ₀, принадлежащих окрестности (x ₀− δ, x ₀ + δ) выполняется неравенство f (x) ≤ f (x ₀). Если для всех точек x ≠ x ₀ из некоторой окрестности точки x ₀ выполняется строгое неравенство f (x) < f (x ₀), то точка x ₀ является точкой строгого локального максимума. Аналогично определяется локальный минимум функции f (x). В этом случае для всех точек x ≠ x ₀ из δ -окрестности (x ₀− δ, x ₀ + δ) точки x ₀ справедливо неравенство f (x) ≥ f (x ₀). Соответственно, строгий локальный минимум описывается строгим неравенством f (x) > f (x ₀). Понятия локального максимума и локального минимума объединяются общим термином локальный экстремум. Слово "локальный" для краткости часто опускают и говорят просто о максимумах и минимумах функции.

Рис.1

На рисунке 1 схематически показаны различные точки экстремума. Точка A (x ₁) является точкой строгого локального минимума, поскольку для нее существует δ -окрестность (x ₀− δ, x ₀ + δ), в которой справедливо неравенство

f (x) > f (x ₁) ∀ x ∈ (x ₁ − δ, x ₁ + δ).