Пусть функция f (x) дифференцируема в некоторой окрестности точки x 0, кроме, быть может, самой точки x 0,в которой, однако, функция непрерывна. Тогда:
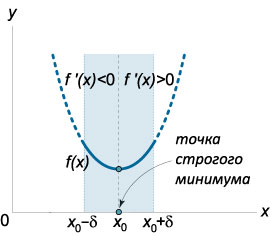
- Если производная f ' (x) меняет знак с минуса на плюс при переходе через точку x 0 (слева направо), то точка x 0 является точкой строгого минимума (рис.2). Другими словами, в этом случае существует число δ > 0, такое, что
∀ x ∈ (x 0 − δ, x 0) ⇒ f ' (x) < 0,
∀ x ∈ (x 0, x 0 + δ) ⇒ f ' (x) > 0.
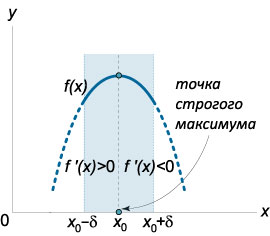
- Если производная f ' (x), наоборот, меняет знак с плюса на минус при переходе через точку x 0, то точка x 0 является точкой строгого максимума (рис.3). Иначе говоря, существует число δ > 0, такое, что
∀ x ∈ (x 0 − δ, x 0) ⇒ f ' (x) > 0,
∀ x ∈ (x 0, x 0 + δ) ⇒ f ' (x) < 0.
 |  | |
| Рис.2 | Рис.3 |
Доказательство.
Ограничимся рассмотрением случая минимума. Пусть производная f ' (x) при переходе через точку x 0 меняет знак с минуса на плюс. Слева от точки x 0 выполняется условие
∀ x ∈ (x 0 − δ, x 0) ⇒ f ' (x) < 0.
По теореме Лагранжа разность значений функции в точках x и x 0 записывается как
f (x) − f (x 0) = f ' (c) (x − x 0),
где точка c принадлежит интервалу (x 0 − δ, x 0), в котором производная отрицательна, т.е. f ' (c) < 0. Поскольку x − x 0 < 0 слева от точки x 0, то следовательно,
f (x) − f (x 0) > 0 для всех x ∈ (x 0 − δ, x 0).
Таким же образом устанавливается, что
f (x) − f (x 0) > 0 для всех x ∈ (x 0, x 0 + δ)
(справа от точки x 0).
На основании определения заключаем, что точка x 0 является точкой строгого минимума функции f (x).
Аналогично можно доказать первое достаточное условие для строгого максимума функции.
Заметим, что в первом достаточном условии не требуется, чтобы функция была дифференцируемой в точке x 0. Если в этой точке производная равна бесконечности или не существует (т.е. точка x 0 является критической, но не стационарной), то первое достаточное условие все равно можно использовать для исследования функции на максимум или минимум.
 2015-04-06
2015-04-06 2194
2194
