Третье достаточное условие экстремума

Пусть функция f (x) имеет в точке x ₀ производные до n -го порядка включительно. Тогда, если

f ' (x ₀) = f '' (x ₀) =... = f ^{(n −1)}(x ₀) = 0 и fⁿ (x ₀) ≠ 0,

то при четном n точка x ₀ является

− точкой строгого минимума, если fⁿ (x ₀) > 0, и
− точкой строгого максимума, если fⁿ (x ₀) < 0.

При нечетном n экстремума в точке x ₀ не существует.

Ясно, что при n = 2 в качестве частного случая мы получаем рассмотренное выше второе достаточное условие экстремума. Чтобы исключить такой переход, в третьем признаке полагают, что n > 2.

Доказательство.
Разложим функцию f (x) в точке x ₀ в ряд Тейлора:

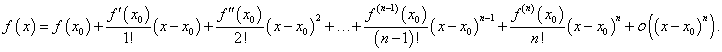
Поскольку по условию теоремы все первые производные до (n − 1)-го порядка равны нулю, получаем:

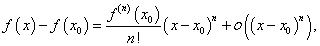
где остаточный член ο ((x − x ₀) ⁿ) имеет более высокий порядок малости, чем n. В результате в δ -окрестности точки x ₀ знак разности f ((x) − f (x ₀) будет определяться знаком n -го члена в ряде Тейлора:

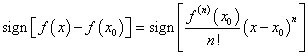
или

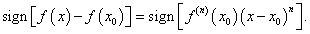
Если n − четное число (n = 2 k), то

∀ x ∈ (x ₀ − δ, x ₀ + δ) ⇒ (x − x ₀)^{2 k} > 0.

Следовательно, в этом случае

sign [ f (x) − f (x ₀)] = sign f ⁽ⁿ⁾(x ₀).

При f ⁽ⁿ⁾(x ₀) > 0 в δ -окрестности точки x ₀ выполняется неравенство

f ((x) − f (x ₀) > 0.

По определению это означает, что x ₀ − точка строгого минимума функции f (x).

Аналогично, при f ⁽ⁿ⁾(x ₀) < 0 в δ -окрестности точки x ₀ имеем неравенство

f ((x) − f (x ₀) < 0,

что соответствует точке строгого максимума.

Если n − нечетное число (n = 2 k + 1), то степень (x − x ₀)^{2 k +1} будет менять знак при переходе через точку x ₀. Тогда из формулы