Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).
Формула Ньютона-Лейбница или основной формулой интегрального исчисления 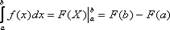
Несобственным называется определённый интеграл, если выполняется, по крайней мере, одно из следующих условий: а)Предел a или b (или оба предела) являются бесконечными;в) Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
Геометрический смысл несобственного интеграла I рода -несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
Геометрический смысл несобственных интегралов II рода -несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
Несобственным интегралом (интегралом первого рода) от функции f(x) на полуинтервале [а, +∞) называется предел
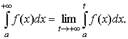
В этом случае говорят, что несобственный интеграл сходится,в противном случае - расходящимся.
Несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси 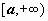 и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла
и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла 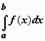 при
при 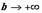 называется несобственным интегралом функции f(x) от a до
называется несобственным интегралом функции f(x) от a до 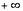 и обозначается
и обозначается 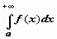 .
.
Несобственным интегралом 2 рода называется 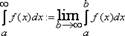
 2015-04-06
2015-04-06 401
401







