Из определения дифференциала функции z=ƒ (х; у) следует, что при достаточно малых |Δх| и |Δу| имеет место приближенное равенство 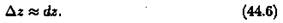
Так как полное приращение Δz=ƒ(х+Δх;у+Δу)-ƒ(х;у), равенство (44.6) можно переписать в следующем виде: 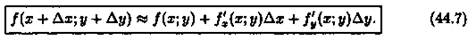
Точка (х0;у0) называется точкой максимума функции z=ƒ(х;у), если существует такая d-окрестность точки (х0;у0), что для каждой точки (х;у), отличной от (хо;уо), из этой окрестности выполняется неравенство ƒ(х;у)<ƒ(хо;уо).
Точка минимума функции: для всех точек (х; у), отличных от (х0;у0), из d-окрестности точки (хо;уо) выполняется неравенство: ƒ(х;у)>ƒ(х0;у0)
Максимумом (минимумом) функции -значение функции в точке максимума (минимума).
Экстремумами -максимум и минимум функции.
_______________________________________________________________________________________
Дифференциальные уравнения - это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. 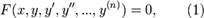 или такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят явно производные искомых функций до некоторого порядка
или такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят явно производные искомых функций до некоторого порядка
Уравнением с разделяющимися переменными - уравнение вида 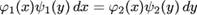 , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от x и только от y
, в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от x и только от y
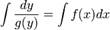
Однородное дифференциальное уравнение первого порядка 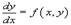
называется однородным, если правая часть удовлетворяет соотношению 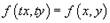 для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y: 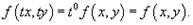 Однородное дифференциальное уравнение можно также записать в виде
Однородное дифференциальное уравнение можно также записать в виде 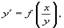 или через дифференциалы:
или через дифференциалы: 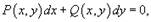
Уравнением Бернулли называется дифференциальное уравнение 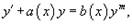 (при n = 0 или n = 1 получаем неоднородное или однородное линейное уравнение).
(при n = 0 или n = 1 получаем неоднородное или однородное линейное уравнение).
Дифференциальными уравнениями высшего порядка называют уравнения порядка выше первого. В общем случае такие уравнения имеют вид F (x, y, y ′, y ′′, K, y (n)) = 0,
Обыкновенным дифференциальным уравнением n -го порядка – Уравнение вида 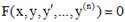 или
или 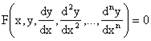 где x - независимая переменная, y - искомая функция, а функция F определена и непрерывна в некоторой области и во всяком случае зависит от
где x - независимая переменная, y - искомая функция, а функция F определена и непрерывна в некоторой области и во всяком случае зависит от 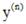
 2015-04-06
2015-04-06 1824
1824
