Ряд 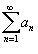 называется абсолютно сходящимся, если ряд
называется абсолютно сходящимся, если ряд 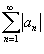 также сходится.
также сходится.
Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
___________________________________________________________________________________________________
Степенной ряд – это ряд, в общий член 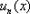 которого входят целые положительные степени независимой переменной
которого входят целые положительные степени независимой переменной  И записывается
И записывается 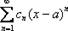
Степенным рядом называется функциональный ряд вида 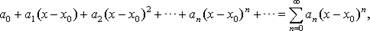
где a0, a1, a2, …,an,…, а также x0 – постоянные числа.
Центром степенного ряда - точку x0
Признак Д’Аламбера: Если при n > N и α > 1 выполнено неравенство 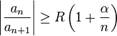 тогда степенной ряд
тогда степенной ряд 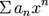 сходится во всех точках окружности | x | = R абсолютно и равномерно по x.
сходится во всех точках окружности | x | = R абсолютно и равномерно по x.
Интервалом сходимости - область определения функции 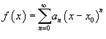 является множество тех значений x, при которых ряд сходится
является множество тех значений x, при которых ряд сходится
Радиусом сходимости - если интервал сходимости представляется в виде 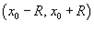 , где R > 0, то величина R
, где R > 0, то величина R
Радиус сходимости вычислить радикальным признаком Коши, по формуле 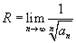
Признака Даламбера: 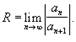
Функциональный ряд -ряд, каждым членом которого является функция 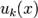 .
.
 2015-04-06
2015-04-06 462
462








