Если ряд 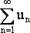 сходится, то
сходится, то 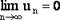 .
.
если 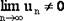 , то ряд расходится.
, то ряд расходится.
Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов.
Признак Даламбера: Положительный числовой ряд 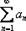 . Если существует предел отношения последующего члена к предыдущему:
. Если существует предел отношения последующего члена к предыдущему: 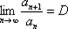 , то:
, то:
а) При D<1 ряд сходится. В частности, ряд сходится при D=0.
б) При D>1 ряд расходится. В частности, ряд расходится при 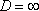 .
.
в) При D=1 признак не дает ответа.
Радикальный признак Коши: Если для ряда 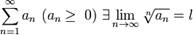
если 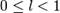 ряд сходится,
ряд сходится,
если l > 1 ряд расходится,
если l = 1 вопрос о сходимости ряда остается открытым
Интегральный признак Коши Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд 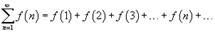 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл 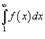 , и расходится, если
, и расходится, если 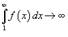 .
.
 2015-04-06
2015-04-06 341
341








