- Найти зависимость частоты колебаний от амплитуды для системы, описываемой уравнением
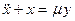 , где
, где 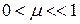 , а функция
, а функция 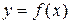 задана уравнениями:
задана уравнениями: 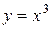 .
.
Решение
Будем решать используя метод медленно меняющихся амплитуд
Будем искать решение в виде:
x=A cos(t + θ(t)) (1)
Первая производная:
x’ = A’(t) cos (t + θ (t)) - A(t) (1 + θ’ (t)) sin (t + θ(t))
Если принять допущение: (т.к. A, θ - медленно меняющиеся функции)
A’(t) cos (t + θ (t)) - A(t) θ’ (t) sin (t + θ(t)) = 0
То производная примет вид:
x’ = -A(t) sin (t + θ(t))
Вторая призводная:
x’’ =- A’(t) sin (t + θ (t)) - A(t) (1 + θ’ (t)) cos (t + θ(t))
Подставив в исходное уравнение, получим:
A’(t) sin (t + θ (t)) + A(t) θ’ (t) cos (t + θ(t)) = - μ y
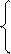 Вместе с принятым допущение получим систему:
Вместе с принятым допущение получим систему:
A’(t) sin (t + θ (t)) + A(t) θ’ (t) cos (t + θ(t)) = - μ y
A’(t) cos (t + θ (t)) - A(t) θ’ (t) sin (t + θ(t)) = 0
Умножая первое на cos (t + θ (t), а второе на sin (t + θ (t) и наоборот и складывая получим систему:
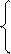 A’ = - μ y sin (t + θ)
A’ = - μ y sin (t + θ)
Аθ’ = - μ y cos (t + θ)
Усредним правые части за период получим систему укороченных уравнений:
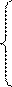 A’ = -
A’ = - 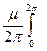 y sin (t1) dt1
y sin (t1) dt1
Аθ’ = - 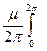 y cos (t1) dt1
y cos (t1) dt1
Где t1 = t + θ
Нам понадобится только второе:
Аθ’ = - 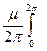 A3 cos3(t1) cos (t1) dt1 = - A3
A3 cos3(t1) cos (t1) dt1 = - A3 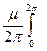
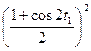 dt1 =
dt1 =
= - A3 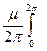
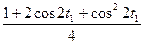 dt1 = - A3
dt1 = - A3 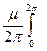
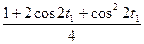 dt1 =
dt1 =
= - A3 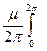
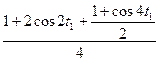 dt1 = -A3
dt1 = -A3 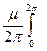
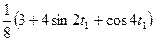 dt1 =
dt1 =
= -A3 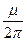
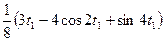
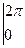 = -
= - 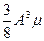
Аθ’ = - 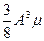 ; θ = -
; θ = - 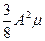 t
t
Подставляем в (1): x=A cos(t - 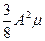 t) = A cos(t (1-
t) = A cos(t (1- 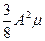 ))= A cos(ωt)
))= A cos(ωt)
Отсюда ответ: ω = 1- 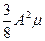
2. Два одинаковых LC контура связаны общей емкостью. Показать, что нормальные моды колебаний описываются формулами 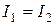 при
при 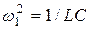 и
и 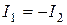 при
при 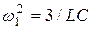 .
. 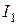 - ток в первом контуре,
- ток в первом контуре, 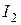 - ток во втором контуре.
- ток во втором контуре.
Решение
|
|
|
|
|

i1=i3+i2, i3=i1-i2 – закон Киргофа
Падение напряжения на катушке
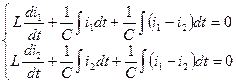
Дифференцируем по t
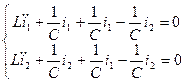
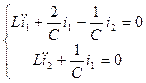
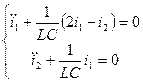
1 случай. I1=I2
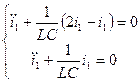
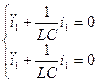
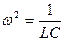 - уравнение гармонического асциллятора
- уравнение гармонического асциллятора
1 случай. I1=-I2
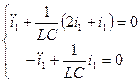
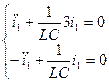
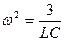 - уравнение гармонического асциллятора
- уравнение гармонического асциллятора
- Получить дисперсионное уравнение и построить дисперсионную характеристику для однородной цепочки.
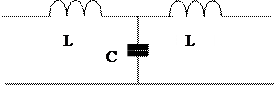 |
i1=i3+i2 - уравнение для токов цепи
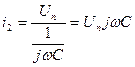 ;
; 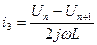 ;
; 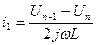
Получаем
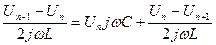
Уравнение для гармонических колебаний напряжения в цепи со сдвигом
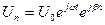
Подставим в уравнение
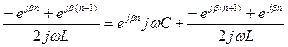
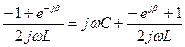
Умножим всё на 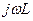
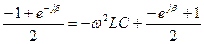
переставим
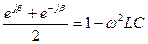 , т.е.
, т.е.
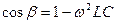
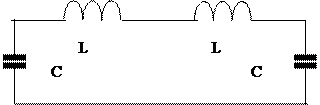
Замкнутый контур, где 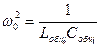
Lобщ=2L; Собщ=С/2
Получаем
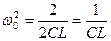
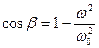
1) 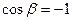 ;
; 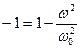 ;
; 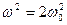 ;
; 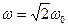 .
.
2) 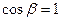 ;
; 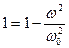 ;
; 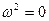 ;
; 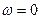 .
.
- Смещение гармонического осциллятора описывается уравнением
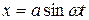 . Считая, что смещение
. Считая, что смещение 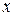 и скорость
и скорость 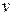 откладываются на двух взаимно перпендикулярных осях, исключите время
откладываются на двух взаимно перпендикулярных осях, исключите время 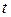 и покажите, что геометрическим местом точек
и покажите, что геометрическим местом точек 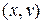 является эллипс. Докажите, что этот эллипс является кривой постоянной энергии.
является эллипс. Докажите, что этот эллипс является кривой постоянной энергии.
Решение.
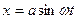
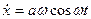
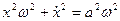
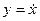
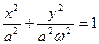 - уравнение эллипса
- уравнение эллипса
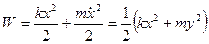
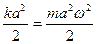 -баланс энергий
-баланс энергий
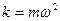 ,
, 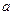 -максимальная амплитуда,
-максимальная амплитуда, 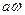 -максимальная скорость
-максимальная скорость
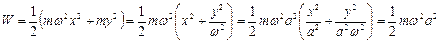 .
.
- Для математического маятника, который колеблется с амплитудой
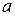 , найти фазовую постоянную для решения:
, найти фазовую постоянную для решения: 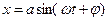 если колебания начинаются из положения
если колебания начинаются из положения 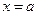 .
.
В начальный момент времени:
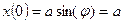
Отсюда:
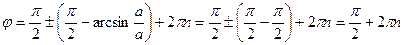 ,
, 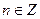
Ответ 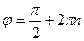 ,
, 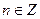
- На цепочку последовательно соединенных катушки индуктивности, конденсатора и резистора подается синусоидальное напряжение с амплитудой
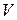 . Покажите, что при резонансе тока напряжение как на катушке индуктивности, так и на конденсаторе равно
. Покажите, что при резонансе тока напряжение как на катушке индуктивности, так и на конденсаторе равно 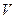 .
.
Решение.
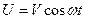
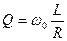 -добротность
-добротность
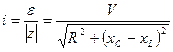 -для тока
-для тока 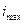
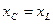
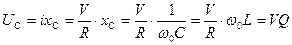
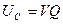
 2015-04-08
2015-04-08 847
847








