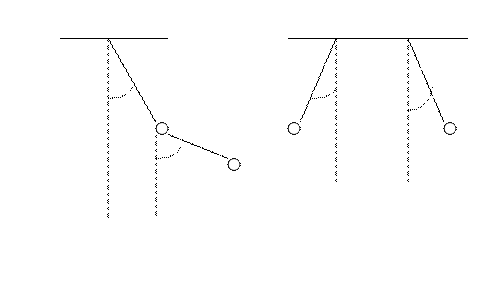
Примеры таких систем показаны на рис. 12.1.
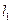
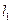
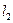
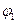
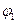
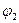
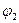
а) б)
Рис.12.1
Данные колебательные системы имеют две степени свободы. При заданных значениях 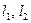 в качестве обобщенных координат можно взять углы отклонения
в качестве обобщенных координат можно взять углы отклонения 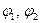 .
.
Многоатомные нелинейные молекулы имеют 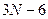 колебательных степеней свободы, линейные многоатомные молекулы имеют
колебательных степеней свободы, линейные многоатомные молекулы имеют 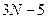 колебательных степеней свободы. Здесь
колебательных степеней свободы. Здесь 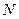 - число атомов в молекуле.
- число атомов в молекуле.
кинетическая энергия системы со многими степенями свободы может быть представлена в виде:
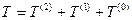 (9.16)
(9.16)
где
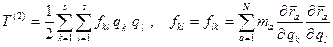 , (9.17)
, (9.17)
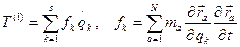 , (9.18)
, (9.18)
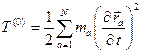 .
.
В том случае, когда на систему накладываются стационарные связи, для кинетической энергии можно записать:
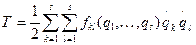 , (9.20)
, (9.20)
и функция Лагранжа, в случае активных потенциальных сил имеет вид:
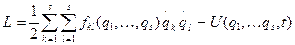 . (9.21)
. (9.21)
Коэффициенты 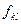 носят название коэффициентов инерции
носят название коэффициентов инерции
Разложим потенциальную энергию в ряд по степеням 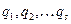 вблизи устойчивого положения равновесия системы:
вблизи устойчивого положения равновесия системы:
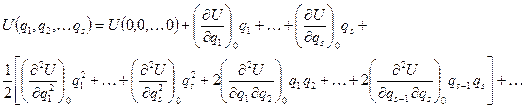
Введем обозначения:
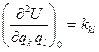 . (12.2)
. (12.2)
Эти коэффициенты называются обобщенными коэффициентами жесткости. Они симметричны, т.е.
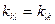 . (12.3)
. (12.3)
В результате для потенциальной энергии получаем:
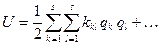 , (12.4)
, (12.4)
где точками обозначены члены высших порядков. Для случая малых колебаний используется гармоническое приближение, в котором всеми, не выписанными членами старших порядков, пренебрегают. В результате функция Лагранжа колебательной системы в гармоническом приближении имеет вид:
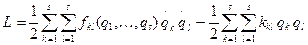 .
.
Рассмотрим систему с двумя степенями свободы, которая совершает малые колебания вблизи устойчивого положения равновесия.
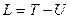 , (12.6)
, (12.6)
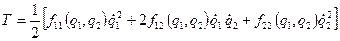 , (12.7)
, (12.7)
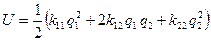 .
.
Дифференциальные уравнения колебаний получаются из уравнений Лагранжа
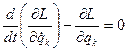 (12.11)
(12.11)
и выражений (12.6), (12.8) и (12.9):
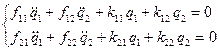 , (12.12)
, (12.12)
где использованы равенства 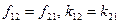 .
.
Следовательно, малые колебания системы с двумя степенями свободы около положения устойчивого равновесия описываются двумя однородными линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами.
Решение уравнений (12.2) ищем в виде:
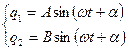 , (12.13)
, (12.13)
где 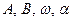 - неизвестные постоянные.
- неизвестные постоянные.
Дифференцируя дважды по времени уравнения (12.13), подставляя полученные результаты в уравнения (12.12), получим:
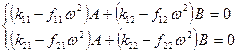 . (12.14)
. (12.14)
Система (12.14) содержит алгебраические однородные линейные уравнения для нахождения амплитуд 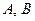 . Система уравнений (12.14) имеет решение отличное от нуля, если определитель этой системы равен нулю:
. Система уравнений (12.14) имеет решение отличное от нуля, если определитель этой системы равен нулю:
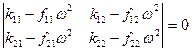 .
.
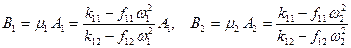 . (12.17)
. (12.17)
И окончательно, общее решение:
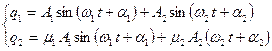
 2015-04-08
2015-04-08 1245
1245
