1. Фаза сигнала φ распределена на интервале [-π, π ] равномерно: 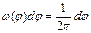 . Найти f(x, y) – совместную плотность вероятности случайных величин x=sin φ, y=cos φ. . Найти f(x, y) – совместную плотность вероятности случайных величин x=sin φ, y=cos φ.
| |
Дано:
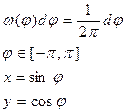
| 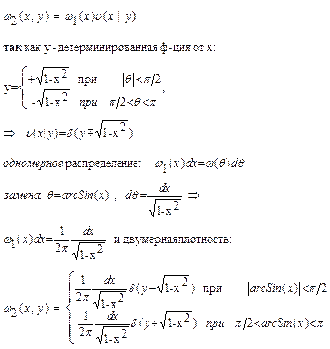
|
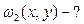
|
2. На вход линейного четырехполюсника, у которого выходное напряжение 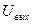 связано с входным напряжением связано с входным напряжением 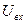 равенством: равенством: 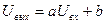 , где a,b=const подается последовательность импульсов, амплитуды которых распределены но нормальному (гауссовому) закону со средней амплитудой , где a,b=const подается последовательность импульсов, амплитуды которых распределены но нормальному (гауссовому) закону со средней амплитудой 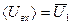 и дисперсией и дисперсией 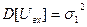 . Найти среднее значение . Найти среднее значение 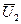 и дисперсию и дисперсию 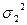 выходного напряжения. выходного напряжения.
| |
Дано:
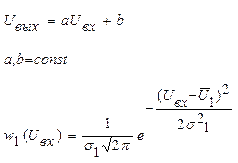
| 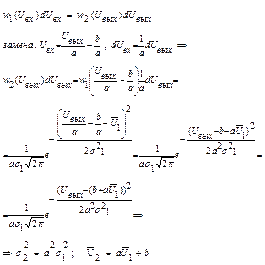
|
Найти:
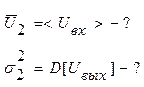
|
3. Случайный процесс u (t) имеет вид 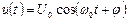 , где U 0,ω0 – фиксированные величины, фаза φ – случайная величина, равномерно распределенная в интервале [-π, π ]. Определить среднее значение , где U 0,ω0 – фиксированные величины, фаза φ – случайная величина, равномерно распределенная в интервале [-π, π ]. Определить среднее значение 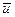 , дисперсию , дисперсию 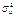 случайного процесса. Доказать, что случайный процесс u (t) стационарен. случайного процесса. Доказать, что случайный процесс u (t) стационарен.
| |
Дано:
Случайный процесс:
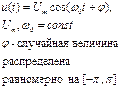
| 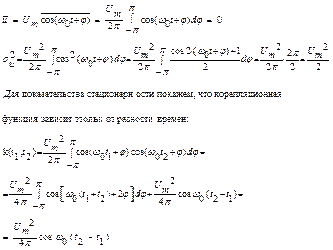
|
Найти:
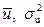 Доказать:
Доказать:
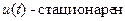
|
| 4. Сигнал представляет собой сумму гармонических колебаний одной и той же частоты. Амплитуды слагаемых величин одинаковы и равны 5В, начальные фазы могут независимо принимать лишь два значения: 0 и π. Число слагаемых равно 30. Вычислить вероятность того, что результирующая амплитуда сигнала окажется больше 40В. | |
Дано:
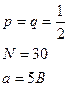
| 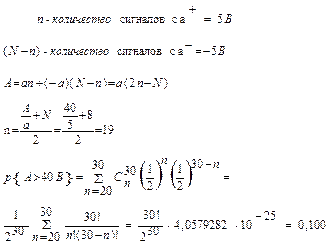
|
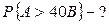
|
5. Использую теорему Винера-Хинчина, найти энергетический спектр стационарного случайного процесса с корреляционной функцией 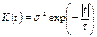 . .
| |
Дано:
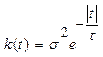
| 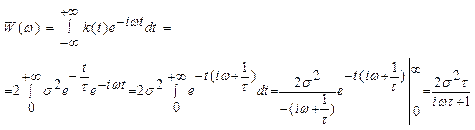
|
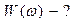
|
6. Пусть стационарный случайный процесс X (t) характеризуется следующим энергетическим спектром: 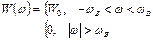 Найти корреляционную функцию процесса X (t)
Найти корреляционную функцию процесса X (t)
| |
Дано:
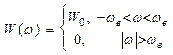
| 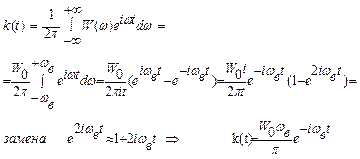
|
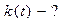
|
7. Пусть узкополосный нормальный (гауссов) процесс имеет постоянное значение одностороннего энергетического спектра 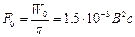 в пределах полосы частот от в пределах полосы частот от 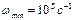 до до 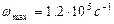 . Найти вероятность того, что огибающая этого процесса будет превосходить уровень . Найти вероятность того, что огибающая этого процесса будет превосходить уровень 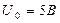
| |
Дано:
Узкополосный Гауссов процесс с односторонним энергетическим спектром -
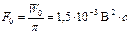 Диапазон частот:
Диапазон частот:
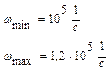
| 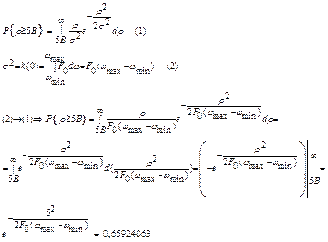
|
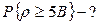
|
8. Найти корреляционную функцию процесса вида «случайного телеграфного сигнала» - случайного процесса 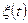 , представляющего собой последовательность скачков между значения + а и – а, причем моменты скачков распределены по закону Пуассона , представляющего собой последовательность скачков между значения + а и – а, причем моменты скачков распределены по закону Пуассона 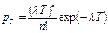 , где λ – среднее число скачков в единицу времени (см. рисунок). , где λ – среднее число скачков в единицу времени (см. рисунок).
| ||
Дано:
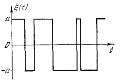 Моменты скачков распределены по:
Моменты скачков распределены по:
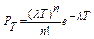
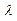 - среднее число скачков в ед. времени - среднее число скачков в ед. времени
| 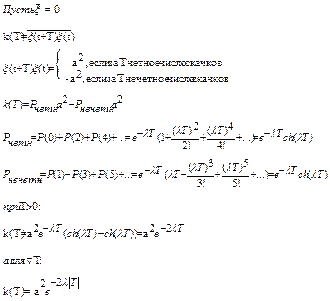
| |
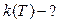
| ||
| 9. Устройство, имеющее два устойчивых состояния (триггер), находится пол воздействием случайной последовательности управляющих импульсов, с одинаковой вероятностью имеющих знаки плюс и минус. Пусть положительный импульс создает или сохраняет состояние 1 триггера, отрицательные – создает или сохраняет состояние 2. Число импульсов, поступающих на триггер в единицу времени, равно а. Считая, что в начальный момент времени триггер находился в состоянии 1, найти вероятность обнаружить триггер в состояниях 1 и 2 в момент времени t. | ||
| Дано: Чья-то отсканеная рукопись | ||
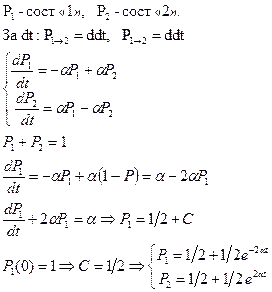
10. Случайная величина ξ имеет нормальное (гауссовое) распределение с математическим ожиданием 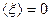 и дисперсией и дисперсией 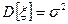 . Доказать, что все моменты . Доказать, что все моменты 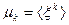 случайной величины ξ выражаются через момент второго порядка случайной величины ξ выражаются через момент второго порядка 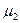 , найти явный вид этих моментов. , найти явный вид этих моментов.
| |
Дано:
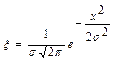
| 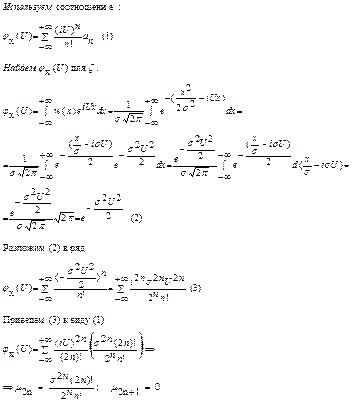
|
Доказать:
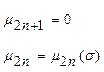
|
Задачи к государственному экзамену по курсу «Электродинамика»
1. Вычислить напряженности электрического и магнитного полей, создаваемых зарядом q, движущимся в постоянной скоростью v.
Преобразования Лоренца:
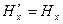
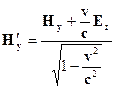
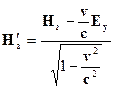
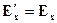
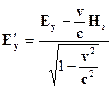
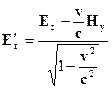
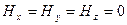
2. В лабораторной системе отсчета наблюдаются два однородных взаимно перпендикулярных векторных поля – электрическое с напряженностью Е и магнитное напряженностью Н, причем ׀ Н׀>׀ Е ׀ (в абсолютной системе единиц). Найти скорость v такой инерциальной системы отсчета, с точки зрения которой в этой лаборатории присутствует только магнитное поле (т.е. Е'= 0) и вычислить напряженность этого поля Н'.
Решение:
Выбираем направление скорости следующим образом 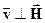 и
и 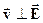
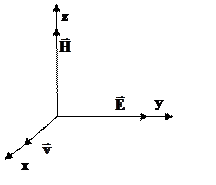
Из рисунка видно, что 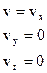
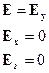
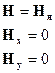
Используя преобразования Лоренца для электромагнитного поля, получаем
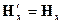
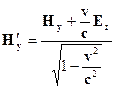
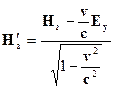
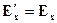
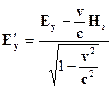
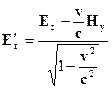

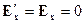
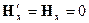
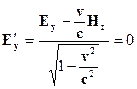
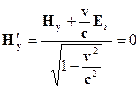
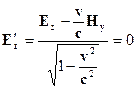
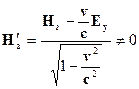
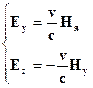
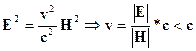
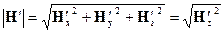
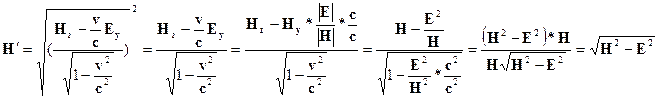
Ответ: 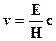
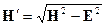
3. По шару радиуса а с одинаковой объемной плотностью распределен заряд q. Пользуясь уравнениями Пуассона и Лапласа, найти потенциал φ вне и внутри шара и по найденному потенциалу определить напряженность поля Е вне и внутри шара. Построить графики зависимости φ и Е от расстояния до центра шара.
Уравнение Пуассона:
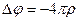
Сферически-симметричное решение:
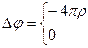
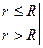 ;
;
Для сферических координат, учитывая что 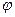 зависит только от радиус вектора
зависит только от радиус вектора 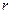 :
:
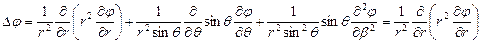
Внутри шара:
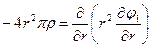 ;
; 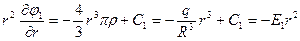 ;
; 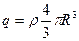
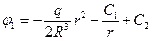 ;
; 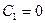 т. к.
т. к. 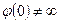 ;
;
Итого: 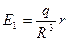 ;
; 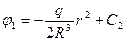
Снаружи шара:
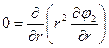 ;
; 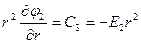 ;
;
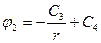 ;
; 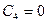 т. к.
т. к. 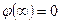 ;
;
Итого: 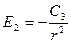 ;
; 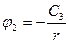
На поверхности шара:
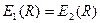 ;
; 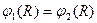
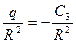 ;
; 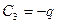
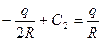 ;
; 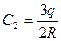
Ответ:
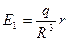 ;
; 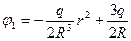
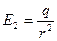 ;
; 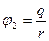
График:
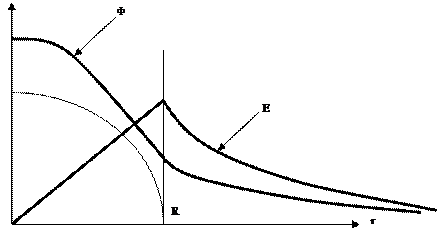
4. По сфере радиуса а с одинаковой поверхностной плотностью распределен заряд q. Пользуясь уравнением Лапласа, найти потенциал φ вне и внутри сферы и по найденному потенциалу определить напряженность поля Е вне и внутри сферы. Построить графики зависимости φ и Е от расстояния до центра сферы.
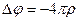
Сферически-симметричное решение:
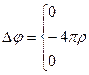
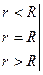 ;
;
Для сферических координат, учитывая что 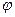 зависит только от радиус вектора
зависит только от радиус вектора 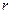 :
:
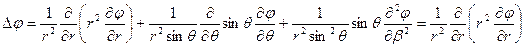
Внутри сферы:
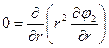 ;
; 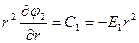 ;
;
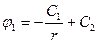 ;
; 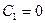 т. к.
т. к. 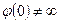 ;
;
Итого: 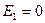 ;
; 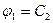
В близи границы сферы применим теорему Гаусса - Остроградского по внешней поверхности сферы:
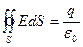 , =>
, => 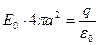
Итого: 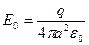
Снаружи сферы:
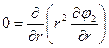 ;
; 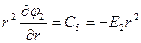 ;
;
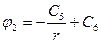 ;
; 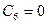 т. к.
т. к. 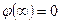 ;
;
Итого: 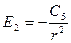 ;
; 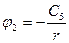
Связываем:
E0 = E2(a) => 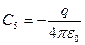
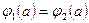 =>
=> 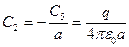
Ответ:
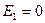 ;
; 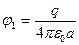
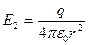 ;
; 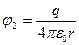
График:

5. Шар радиуса а равномерно заполнен статическим электрическим зарядом с постоянной плотностью ρ – за исключением находящейся внутри шара пустой сферической полости радиуса b. Расстояние между центрами шара и полости d. Найти напряженность поля Е внутри полости.
 Для равномерно заряженного шара напряженность внутри него определяется формулой:
Для равномерно заряженного шара напряженность внутри него определяется формулой:
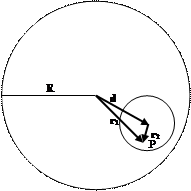
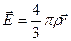
Возьмем точку P внутри полости. Расстояние от центра сферы до точки P:
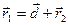 ;
;
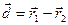
Напряженность в этой точке при условии, что полость тоже заполнена объемным зарядом – векторная сумма напряженности искомой (с пустой полостью) и напряженности, создаваемой только одной заполненной полостью:
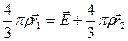 ;
;
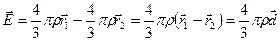

Ответ: 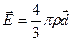
 2015-04-08
2015-04-08 504
504







