2015-04-08
422
Архитектура цифровых устройств базируется на многократном повторении относительно простых базовых логических элементов. Связи между этими элементами строятся на основе формальных методов булевой алгебры (названной так по имени автора – английского математика Джорджа Буля, 1815–1864 гг.) или алгебры логики.
В отличие от обычной алгебры булева алгебра оперирует с логическими переменными, которые могут иметь только два значения: логический нуль «0» и логическая единица «1».
В алгебре логики существуют три простейших операции (функции) над логическими переменными:
1. Логическое отрицание, или инверсия – изменяет значение логической переменной на противоположное значение. В булевых выражениях обозначается чертой над переменной: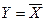 
. В схемотехнике устройство, реализующее операцию отрицания, обозначается словом «NOT», в отечественном варианте «НЕТ». В табл. 1.1 приведены все возможные значения логического отрицания;
Таблица 1.1
Таблица истинности операции логического отрицания (инверсии)
|
|
|
| Х | Y |
2. Логическое умножение, или конъюнкция. Выражение записывается следующим образом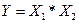 
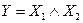или 
или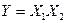 
. Все возможные варианты логического умножения двух переменных приведены в табл. 1.2.
Таблица 1.2.
Таблица истинности операции логического умножения (конъюнкции)
| Х1 | Х2 | Y1 |
3. Логическое сложение, или дизъюнкция. Выражение записывается следующим образом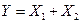 
или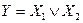 
. Варианты для двух переменных приведены в табл. 1.3.
Таблица 1.3
Таблица истинности операции логического сложения (дизъюнкции).
| Х1 | Х2 | Y1 |
По существу рассмотренные переменные являются булевыми функциями. Первая от одной переменной, последние от двух переменных. Функции, так же как и переменные, могут принимать только два значения «1» и «0».
Для двух переменных существуют 16 функций табл. 1.4.
Таблица 1.4
Булевы функции двух переменных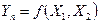 
| Функция | Значение функции при: | Обозначение функции | Название функции | |||
| Х1 =0 | Х1 =0 | Х1 =1 | Х1 =1 | |||
| Х2 =0 | Х2 =1 | Х2 =0 | Х2 =1 | |||
| Y0 | 0 | Константа 0 | ||||
| Y1 | Х1Х2 | Конъюнкция | ||||
| Y2 | Х1DХ2 | Запрет по Х2 | ||||
| Y3 | Х1 | Переменная Х1 | ||||
| Y4 | Х2DХ1 | Запрет по Х 1 | ||||
| Y5 | Х2 | Переменная Х2 | ||||
| Y6 | Х1ÅХ2 | Исключающее ИЛИ | ||||
| Y7 | Х1+Х2 | Дизъюнкция | ||||
| Y8 | Х1¯Х2 | Стрелка Пирса | ||||
| Y9 | Х1~ Х2 | Эквивалентность | ||||
| Y10 |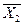 
| Отрицание Х2 | ||||
| Y11 | Х2®Х1 | Импликация от Х2 к Х1 | ||||
| Y12 |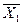 
| Отрицание Х1 | ||||
| Y13 | Х1®Х2 | Импликация от Х1 к Х2 | ||||
| Y14 | Х1/Х2 | Штрих Шеффера | ||||
| Y15 | 1 | Константа 1 |
Для решения конкретных задач могут быть сконструированы новые булевы функции из других булевых функций с помощью суперпозиции. Она состоит в подстановке вместо аргументов других булевых функций. Такая подстановка возможна, так как булевы функции, как и переменные, могут принимать только значения «1» и «0».
|
|
|
В практике, наибольшее применение находят в первую очередь простейшие, а именно Y1 – конъюнкция и Y7 – дизъюнкция, а также еще три, полученные путем суперпозиции простейших:
ü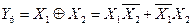 
- исключающее ИЛИ(«сумма по модулю 2»);
ü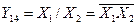 
- штрих Шиффера («И-НЕ»);
ü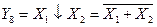 
- стрелка Пирса («ИЛИ-НЕ»).
В современных условиях для проектирования цифровых устройств на ПЛИС разработчику достаточно знать условные обозначения элементов и их функции. Эти данные представлены в табл.1.5.
Таблица 1.5
Схемные элементы, реализующие логические функции
| № п/п | Название функции | Отечественный вариант | Пакет Quartus II | ||
| название элемента | схемное обозначение | название элемента | схемное обозначение | ||
| 1. | Общий корпус |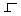 
| gnd |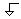 
| |
| 2. | +5В, и т.п. |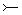 
| vcc |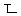 
| |
| 3. | Х | Повторитель |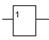 
| buf |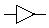 
|
| 4. | Инвертирование Х (НЕ) | НЕ |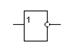 
| not |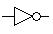 
|
| 5. | Умножение (операция И) | 2И, 3И, … |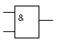 
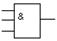
| and2, and3, … |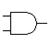 
|
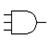
| 6. | Сложение (операция ИЛИ) | 2ИЛИ, 3ИЛИ, … |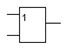 
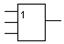
| or2, or3, … |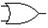 
|
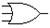
| 7. | Исключающее ИЛИ |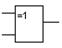 
| xor |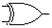 
| |
| 8. | Умножение и отрицание (И-НЕ) | 2И-НЕ, 3И-НЕ, … |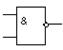 
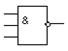
| nand2, nand3, … |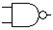 
|
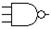
| 9. | Сложение и отрицание (ИЛИ-НЕ) | 2ИЛИ-НЕ, 3ИЛИ-НЕ, … |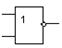 
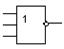
| nor2, nor3, … |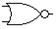 
|
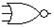
Прежде чем реализовать требуемую функцию с помощью схемных элементов, логическое выражение, представляющее функцию, необходимо привести к виду с минимальным количеством операций. Для этого исходное выражение подвергают преобразованиям в соответствии с законами булевой алгебры. Эти законы, кроме 4 и 5, имеют две формы: для конъюнкции и дизъюнкции. Законы представлены ниже.
