Говорят, что функция z = f(x, y) имеет максимум в точке М0(х0, у0), если f(x0, y0) > f(x, y) и минимум, если f(x0, y0) < f(x, y) для всех точек, достаточно близких к М0 и отличных от нее. Максимум и минимум называют экстремумами функции. Экстремумы можно определить и иначе: Положим х = х0 + Dх и у = у0 + Dу, тогда f(х+ Dх, у + Dу) – f(х0, у0) = Df. Если Df > 0 при всех достаточно малых приращениях независимых переменных, то функция f(x, y) достигает минимума в точке М0. Если Df < 0 при всех достаточно малых приращениях аргументов, то функция f(x, y) достигает максимума в точке М0.
Определения эти справедливы для функций любого числа переменных. Необходимое условие экстремума можно сформулировать так:
Если функция z = f(x, y) достигает экстремума при х = х0, у = у0, то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не существует.
Действительно, если функция z = f(x, y) имеет в некоторой точке М0(х0,у0) экстремум, в этой точке имеют экстремум и функции одной переменной z = f(х0, у) и z = f(х, у0) и, соответственно, их производные 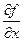 и
и 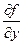 в этой точке или равны нулю или не существуют. Точки, в которых выполняются эти условия, называются критическими, и в этих точках может быть (а может и не быть) экстремум. Критические точки, в которых zx` = 0 и zу` = 0 называют стационарными. О наличии экстремума в стационарных точках можно во многих случаях судить на основании следующей теоремы:
в этой точке или равны нулю или не существуют. Точки, в которых выполняются эти условия, называются критическими, и в этих точках может быть (а может и не быть) экстремум. Критические точки, в которых zx` = 0 и zу` = 0 называют стационарными. О наличии экстремума в стационарных точках можно во многих случаях судить на основании следующей теоремы:
Если в некоторой области, содержащей точку М0(х0, у0), функция имеет непрерывные частные производные до третьего порядка включительно и точка М0 является стационарной, то в этой точке:
Функция имеет максимум, если D> 0, а A < 0 или (C < 0)
Функция имеет минимум, если D> 0, а A > 0 или (C > 0)
Функция не имеет экстремума, если D< 0
Если D = 0 – сомнительный случай, требуется дополнительное исследование.
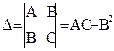 (4.12), где:
(4.12), где: 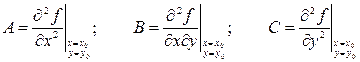
 2015-04-20
2015-04-20 346
346








