Экстремумы функции нескольких независимых переменных называются абсолютными.
Аргументы функции нескольких переменных могут быть связаны некими соотношениями (условиями). В этом случае экстремумы функции f(x,y) называют условными или относительными. Рассмотрим ситуацию на примере функции двух переменных.
Поставим задачу: найти наибольшее и наименьшее значение функции f(x,y) в некоторой замкнутой области. Задача решается в два этапа. Сначала мы ищем абсолютные экстремумы внутри области. Затем находим условные экстремумы на границах области. (Уравнения границ и есть условия, связывающие аргументы функции f(x,y)). Из найденных значений (абсолютных экстремумов внутри области и условных на границах ее) выбирают наибольшее и наименьшее.
Пусть на плоскости х0у дан треугольник АОВ, образованный осями координат Ох (у = 0), Оу (х = 0) и прямой х + у – 1 = 0. Найдем точку С треугольника, для которой сумма квадратов расстояний ее от вершины треугольника (обозначим ее через Z) была бы наименьшей.
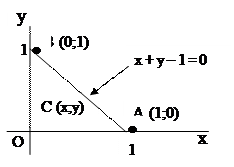 Рис. 4.4 Рис. 4.4 | Z = OC2 + OB2 + OA2 = = x2 + y2 + (x – 1)2 + y2 + x2 + (y – 1) откуда Z = 2x2 + 2y2 + (x – 1)2 + (y – 1)2 Найдем абсолютные экстремумы внутри рассматриваемой области. 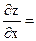 4х + 2(х – 1) = 6х – 2; 4х + 2(х – 1) = 6х – 2; 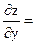 4у + 2 (у – 1) = 6у – 2 4у + 2 (у – 1) = 6у – 2 |

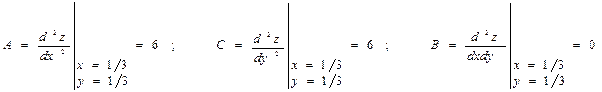
∆ = АС – В2 = 36 > 0; А > 0 и, следовательно, в точке 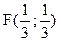 функция
функция
Z = f(x,y) имеет минимум 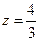 .
.
Найдём условные экстремумы на границах области.
1. Прямая ОА; у=0; 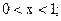 Подставляя уравнение границы в
Подставляя уравнение границы в 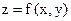 получим функцию одной переменной
получим функцию одной переменной 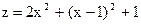 и найдём её экстремум
и найдём её экстремум 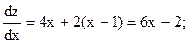 Критическая точка:
Критическая точка: 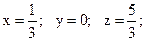
2. Прямая ОВ; х=0; 
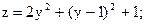
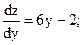 Критическая точка
Критическая точка 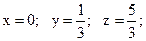
3. Прямая АВ; 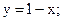
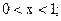
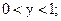
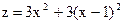 ;
; 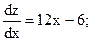 Критическая точка
Критическая точка 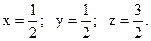
Сравнивая полученные значения абсолютного и условных экстремумов находим наименьшее значение функции в замкнутой области 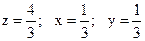 .
.
Рассмотренный способ отыскания условного экстремума не всегда пригоден. (Например, если уравнение границы области задано неявной функцией 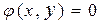 , неразрешимой относительно переменных). В этом случае целесообразно использовать способ множителей Лагранжа. Рассмотрим его на примере функции двух переменных.
, неразрешимой относительно переменных). В этом случае целесообразно использовать способ множителей Лагранжа. Рассмотрим его на примере функции двух переменных.
Найдём экстремум функции 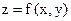 (1) при условии, что х и у связаны уравнением
(1) при условии, что х и у связаны уравнением 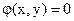 (2). Напомним, что при значениях х, соответствующих стационарным точкам,
(2). Напомним, что при значениях х, соответствующих стационарным точкам, 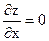 . Найдём
. Найдём 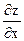 помня, что у есть функция от х:
помня, что у есть функция от х: 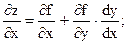 В точках экстремума
В точках экстремума 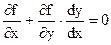 (3). Из (2) находим
(3). Из (2) находим 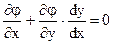 (4). Это равенство справедливо для всех х и у, удовлетворяющих (2). Умножив (4) на неопределённый коэффициент
(4). Это равенство справедливо для всех х и у, удовлетворяющих (2). Умножив (4) на неопределённый коэффициент 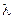 (его и называют м ножителем Лагранжа) и сложив результат с (3) получим:
(его и называют м ножителем Лагранжа) и сложив результат с (3) получим:
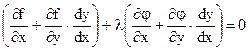 ,
, 
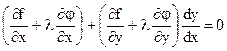 (5).
(5).
Это равенство выполняется во всех точках экстремума. Подберём l так, чтобы в точках экстремума функции z, вторая скобка в (5) обратилась в нуль. (Без потери общности полагаем, что в критических точках 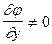 ). Тогда (при значениях х и у соответствующих экстремумам) из (5) следует равенство
). Тогда (при значениях х и у соответствующих экстремумам) из (5) следует равенство 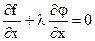 .
.
Получаем систему из трёх уравнений с тремя неизвестными 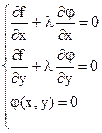 (6) Левые части уравнений системы (6) представляют собой частные производные функции
(6) Левые части уравнений системы (6) представляют собой частные производные функции 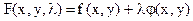 (7) по переменным х, у, l. Уравнения системы являются необходимыми условиями относительногоэкстремума. Чтобы найти наибольшее и наименьшее значения функции в замкнутой области надо:
(7) по переменным х, у, l. Уравнения системы являются необходимыми условиями относительногоэкстремума. Чтобы найти наибольшее и наименьшее значения функции в замкнутой области надо:
1. Найти стационарные точки и вычислить значения функции в них.
2. Найти наибольшее и наименьшее значения функции на границах области.
3. Из всех найденных значений выбрать наибольшее и наименьшее.
Рассмотренный метод исследования на условный экстремум легко распространяется на функции произвольного числа переменных.
Пример: Из данного куска жести площадью 2а надо сделать закрытую коробку в форме прямоугольного параллелепипеда максимального объёма, т.е. надо найти максимум функции 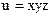 , где (
, где (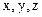 - размеры) при условии что
- размеры) при условии что 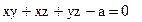
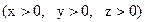 (10). Составим вспомогательную функцию
(10). Составим вспомогательную функцию 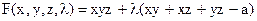 . Найдя её частные производные и приравняв их нулю получим ещё три уравнения (относительно
. Найдя её частные производные и приравняв их нулю получим ещё три уравнения (относительно  и l).
и l).
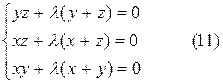 .
.
|
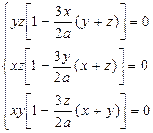
х, у, z по смыслу задачи отличны от нуля, следовательно,
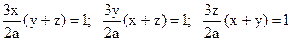 . Из первых двух уравнений находим х = у, из второго и третьего у = z. Из (10) получим
. Из первых двух уравнений находим х = у, из второго и третьего у = z. Из (10) получим 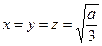 . Это единственная система значений х, у, z при которых может быть максимум или минимум. Из геометрических соображений очевидно, что это максимум (набор единствен, размер коробки ограничен и при каких-то размерах максимален).
. Это единственная система значений х, у, z при которых может быть максимум или минимум. Из геометрических соображений очевидно, что это максимум (набор единствен, размер коробки ограничен и при каких-то размерах максимален).
 2015-04-20
2015-04-20 1577
1577
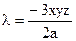 . Подставляя в (11) получим:
. Подставляя в (11) получим: