Для изучения оснащения заводов основными производственными фондами было проведено 10 % -ное выборочное обследование, в результате которого получены следующие данные о распределении заводов по стоимости основных производственных фондов:
| Среднегодовая стоимость основных производственных фондов, млн. сомони | до 2 | 2-4 | 4-6 | свыше 6 | Итого |
| Число заводов |
Требуется определить: 1) с вероятностью 0,997 предельную ошибку выборочной средней и границы, в которых будет находиться среднегодовая стоимость основных производственных фондов всех заводов генеральной совокупности; 2) с вероятностью 0,954 предельную ошибку выборки при определении доли и границы, в которых будет находиться удельный вес заводов со стоимостью основных производственных фондов свыше 4 млн. руб.
Решение:
Предельная ошибка выборки (ошибка репрезентативности) исчисляется по формуле:
∆=± t·µ,
где µ - средняя ошибка репрезентативности;
t – коэффициент кратности ошибки, показывающий, сколько средних ошибок содержится в предельной ошибке.
Пределы возможной ошибки (∆) определяются с вероятностью. Значение t найдем по таблице интеграла вероятностей.
| Для | Соответствует вероятность |
| t=1 | Р=0,683 |
| t=2 | Р=0,954 |
| t=3 | Р=0,997 и т.д. |
Конкретное количественное выражение предельная ошибка принимает после определения средней ошибки выборки. Для нахождения ошибки репрезентативности собственно-случайной и механической выборок имеются следующие формулы:
| Повторная выборка при определении: | |
| Среднего размера ошибки признака | 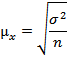
|
| Средней ошибки доли признака | 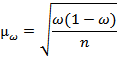
|
| Бесповторная выборка при определении: | |
| Среднего размера ошибки признака | 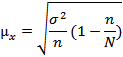
|
| Средней ошибки доли признака | 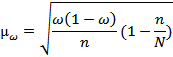
|
1. Для определения границ генеральной средней необходимо исчислить среднюю выборочную (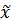 ) и дисперсию (
) и дисперсию (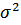 ), техника расчета которых приведена в таблице:
), техника расчета которых приведена в таблице:
| Среднегодовая стоимость основных производственных фондов, млн. сомони, х | Число заводов, f | Середина интервала, х | 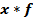
| 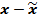
| 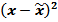
| 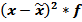
|
| до 2 | -3,52 | 12,39 | 61,95 | |||
| 2,0 - 4,0 | -1,52 | 2,31 | 27,72 | |||
| 4,0 – 6,0 | 0,48 | 0,23 | 5,29 | |||
| свыше 6,0 | 2,48 | 6,15 | 61,50 | |||
| 156,46 |
Тогда
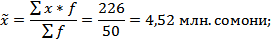
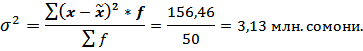
Средняя ошибка выборки при определении среднегодовой стоимости основных фондов составит:
а) при повторном отборе 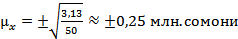
б) при бесповторном отборе 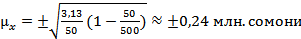
Следовательно, при определении среднегодовой стоимости основных производственных фондов в среднем мы могли допустить среднюю ошибку репрезентативности в 0,25 млн. сомони при повторном и 0,24 млн. сомони при бесповторном отборе в ту или иную сторону о среднегодовой стоимости основных производственных фондов, приходящейся на один завод в выборочной совокупности. Исчисленные данные показывают, что при бесповторной выборке средняя ошибка репрезентативности (0,24) меньше, чем при тех же условиях при повторном отборе (0,25).
В нашем примере Р=0,997, следовательно, t=3.
Исчислим предельную ошибку выборочной средней(∆ х):
∆ х =±3µ, т.е. ∆ х =±3·0,25=±0,75 млн. сомони (при повторном отборе); ∆ х =±3·0,24=±0,72 млн. сомони (при бесповторном отборе).
Порядок установления пределов, в которых находится средняя величина изучаемого показателя в генеральной совокупности в общем виде, может быть представлена следующим образом:
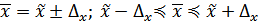
Для нашего примера среднегодовая стоимость основных производственных фондов в среднем на один завод генеральной совокупности будет находиться в следующих пределах:
а) при повторном отборе – 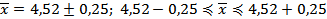
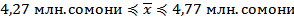
б) при бесповторном отборе - 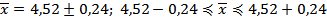
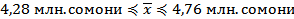
Эти границы можно гарантировать с вероятностью 0,997.
2. Вычисление пределов при установлении доли осуществляется аналогично нахождению пределов для средней величины. В общем виде расчет можно представить следующим образом:
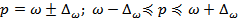
где р – доля единиц, обладающих данным признаком в генеральной совокупности.
Доля заводов в выборочной совокупности со стоимостью основных производственных фондов свыше 4 млн. сомони составляет:
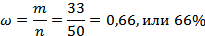
Определяем предельную ошибку доли. По условию задачи известно, что N =500; n =50; ω =0,66; Р =0,954; t =2.
Исчислим предельную ошибку доли:
при повторном отборе 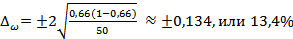 ;
;
при бесповторном отборе 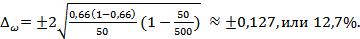
Следовательно, с вероятностью 0,954 доля заводов со стоимостью основных производственных фондов свыше 4 млн. сомони в генеральной совокупности будет находиться в пределах:
р =66%±13,4%, или 52,6% 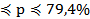 при повторном отборе;
при повторном отборе;
р =66%±12,7%, или 53,3% 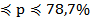 при бесповторном отборе.
при бесповторном отборе.
Расчеты убеждают в том, что при бесповторном отборе ошибка выборки меньше, чем при тех же условиях при повторной выборке.
 2015-04-30
2015-04-30 2675
2675








