Пример 4. В целях контроля качества комплектующих изделий из партии изделий, упакованных в 50 ящиков по 20 изделий в каждом

В целях контроля качества комплектующих изделий из партии изделий, упакованных в 50 ящиков по 20 изделий в каждом, была проведена 10%-ная серийная выборка. По попавшим в выборку ящикам среднее отклонение параметров изделия от нормы соответственно составило 9мм, 11, 12, 8 и 14мм. С вероятностью 0,954 определите среднее отклонение параметров по всей партии в целом.

Решение:

Рассчитаем выборочную среднюю:

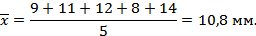
Определим величину межгрупповой дисперсии:

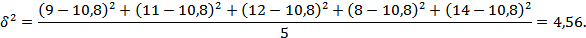
С учетом установленной вероятности р =0,954 (t =2) предельная ошибка выборки составит:

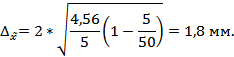
Произведенные расчеты позволяют заключить, что среднее отклонение параметров всех изделий от нормы находиться в следующих границах:

(10,8-1,8)мм ≼ 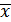≼(10,8+1,8)мм

9,0мм ≼ 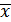≼12,6 мм

Для определения необходимого объема серийной выборки при заданной предельной ошибке используются следующие формулы:

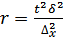– повторный отбор;

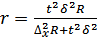– бесповторный отбор.

[1] При наличии необходимой информации отбор также может производиться пропорционально вариации изучаемого признака в группах.