На заводе 1000 рабочих вырабатывают одноименную продукцию. Из них со стажем работы до пяти лет трудятся 400 чел., а более пяти – 600 чел. Для изучения среднегодовой выработки и установления доли квалифицированных рабочих проведена 10% - ная типическая выборка с отбором единиц пропорционально численности рабочих по указанным группам (внутри групп применялся случайный метод отбора).
На основе обследования получены следующие данные:
| Группы рабочих со стажем работы | Общая числен ность рабочих, чел., N | Число обследован ных рабочих, чел., n | Средне
дневная выработ
ка, шт., 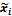
| Диспер
сия выработки, число 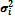
| Число квалифици рованных рабочих в выборке, чел., m | Доля квалифи
цирован
ных рабочих,
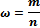
|
| до 5 лет (включительно) | 0,8 | |||||
| свыше 5 лет | 0,9 | |||||
| ИТОГО: |
Определим: 1) с вероятностью 0,954 предельную ошибку выборки и гарницы, в которых будут находиться среднедневная выработка всех рабочих завода; 2) с той же вероятностью пределы удельного веса квалифицированных рабочих в общей численности рабочих завода.
Решение:
1) Средняя ошибка типической выборки определяется по формуле:
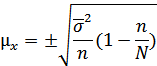
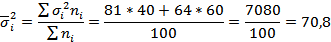
Определим среднюю ошибку выборки при бесповторном отборе:
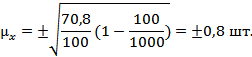
Техника расчета предельной ошибки при типической выборке аналогична расчету предельной ошибки при случайном отборе:
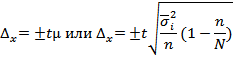
Подставив данные, получим: 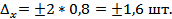
Для определения возможных пределов среднедневной выработки всех рабочих завода первоначально нужно исчислить среднедневную выработку в выборочной совокупности по средней арифметической взвешенной:
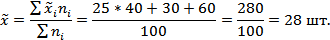
Пределы среднедневной выработки всех рабочих завода: 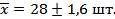
С вероятностью 0,954 можно утверждать, что среднедневная выработка всех рабочих завода находится в пределах 26,4 шт≼ 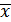 ≼29,6 шт.
≼29,6 шт.
2) Средняя ошибка репрезентативности для доли исчисляется по формуле:
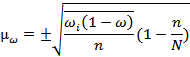
где 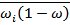 – дисперсия доли (
– дисперсия доли (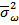 ) является средней из внутригрупповых дисперсий.
) является средней из внутригрупповых дисперсий.
Эта величина исчисляется по формуле:
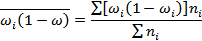
Технику расчета покажем в таблице:
| Группы рабочих со стажем работы | Числен ность рабочих, чел., ni | Доля квалифицирован
ных рабочих, 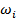
| Доля мало квали
фициро
ванных рабочих 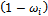
| Дисперсия доли, 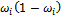
| Взвешенный показатель дисперсии, 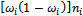
|
| до 5 лет (включительно) | 0,8 | 0,2 | 0,16 | 6,4 | |
| свыше 5 лет | 0,9 | 0,1 | 0,09 | 5,4 | |
| ИТОГО: | 11,8 |
Тогда 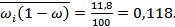
Определим среднюю ошибку репрезентативности для доли:
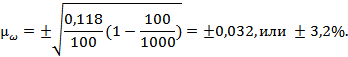
Исчислим предельную ошибку выборочной доли с вероятностью 0,954:
∆ω=± 2·0,032=±0,064, или 6,4%.
Расчет предела при установлении доли в общем виде представляется следующим образом:
р = 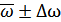
Определим среднюю долю выборочной совокупности:
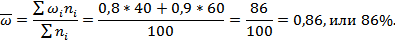
Отсюда: р =86%±6,4%.
С вероятностью 0,954 можно утверждать, что доля квалифицированных рабочих на заводе будет находиться в пределах 79,6%≼ р ≼92,4%.
При определении необходимого объема типической выборки учитывается средняя из внутригрупповых дисперсий:
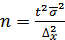 – повторный отбор;
– повторный отбор;
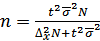 – бесповторный отбор.
– бесповторный отбор.
Полученное значение общего объема выборки необходимо распределить по типическим группам пропорционально их численности.
Серийная выборка. Эта выборка используется в тех случаях, когда единицы изучаемой совокупности объединены в небольшие равновеликие группы или серии. Единицей отбора в этом случае является серия. Серии отбираются с использованием собственно-случайной либо механической выборки, а внутри отобранных серий обследуются все без исключения единицы.
В основе расчета средней серийной выборки лежит межгрупповая дисперсия:
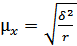 – повторный отбор;
– повторный отбор;
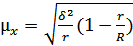 – бесповторный отбор,
– бесповторный отбор,
где 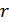 – число отобранных серий;
– число отобранных серий;
R – общее число серий.
Межгрупповую дисперсию при равновеликих группах вычисляют следующим образом:
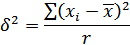
где 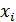 - средняя i -й серии;
- средняя i -й серии;
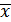 – общая средняя по всей выборочной совокупности.
– общая средняя по всей выборочной совокупности.
 2015-04-30
2015-04-30 2474
2474








