К методам детерминированного факторного анализа относятся: методы цепных подстановок, абсолютных и относительных разниц, индексный, интегральный и логарифмический метод, метод пропорционального деления или долевого участия.
1. Метод цепных подстановок - это один из главных инструментов анализа влияния факторов на результативный показатель, что объясняется его простотой и естественностью. Вместе с тем он имеет и недостатки.
Наиболее существенным из них является неоднозначность этого метода. Значение влияний факторов на результативный показатель зависит от последовательности подстановок. С ростом числа факторов количество возможных подстановок расчет чрезвычайно быстро: для N факторов оно равно N!. Можно построить примеры, в которых последовательность подстановки меняет влияние фактора.
Однако, большинство формул, используемых в анализе, а также пределы изменений факторов таковы, что различия между влияниями одного и того же фактора в зависимости от последовательности подстановок минимальны и часто даже не превышают ошибок округления при вычислениях. Поэтому во многих случаях метод цепных подстановок вполне эффективен.
Метод цепных подстановок является наиболее универсальным, гак как используется для расчета влияния факторов во всех типах детерминированных факторных моделей.
Он состоит в последовательной замене базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде, при этом делается допущение, что значения других факторов остаются неизменными. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются.
Постановка задачи:
Рассмотрим трех факторную мультипликативную модель. Тогда, Yo = f(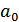 ,
, 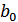 ,
, 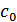 ) – базисное значение результативного показателя,
) – базисное значение результативного показателя,
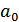 , b0,
, b0, 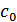 - базисные значения факторов а, b, с.
- базисные значения факторов а, b, с.
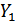 =f(a1,
=f(a1, 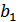 ,
, 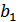 )- фактическое значение результативного показателя,
)- фактическое значение результативного показателя,
а1, b1, c1- фактические значения факторов a, b, с.
Необходимо определить
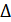 Y=
Y= 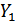 - Y0=
- Y0= 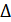 Ya +
Ya + 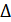 Yb+
Yb+ 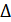 YC
YC
1) Определяем 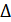 Ya- изменение результативного показателя под влиянием изменения величины факторного показателя а
Ya- изменение результативного показателя под влиянием изменения величины факторного показателя а
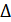 Ya= Ya - Y0= f (
Ya= Ya - Y0= f (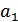 ,
, 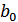 ,
, 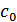 ) - f (
) - f (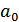 ,b0,
,b0, 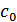 )
)
2) Определяем 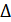 Yb- изменение результативного показателя под влиянием изменения величины факторного показателя b
Yb- изменение результативного показателя под влиянием изменения величины факторного показателя b
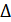 Yb= Yb- Ya= f (
Yb= Yb- Ya= f (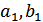 ,
, 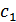 ) – f (
) – f (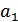 ,
, 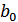 ,
, 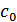 )
)
3) Определяем 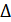 YC- изменение результативного показателя под влиянием изменения величины факторного показателя с
YC- изменение результативного показателя под влиянием изменения величины факторного показателя с
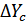 =
= 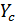 -
- 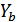 = f (
= f (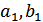 ,
, 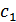 ) –f (
) –f (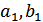 ,
, 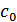 ).
).
 2015-04-30
2015-04-30 630
630








