Этот метод анализа является обобщением метода цепных подстановок. В случае изменения последовательности вычислений в отличие от метода цепных подстановок он не оказывает влияния на конечные результаты расчета.
Расчеты, связанные с использованием интегрального метода, требуют знания основ математического анализа, и предполагает выполнение значительного объема вычислений по сравнению с методом цепных подстановок. Наиболее распространенные формулы приводятся ниже.
1) Двухфакторная мультипликативная модель:
y = 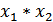
Влияние факторов определяется по формулам:
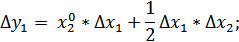
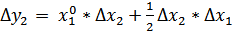 .
.
2) Трехфакторная мультипликативная модель:
y = 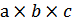
Δya= 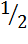 Δa(b0c1+b1c0)+
Δa(b0c1+b1c0)+ 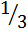 ΔaΔbΔc;
ΔaΔbΔc;
Δyb= 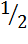 Δb(a0c1+a1c0)+
Δb(a0c1+a1c0)+ 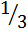 ΔaΔbΔc;
ΔaΔbΔc;
Δyc= 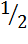 Δc(a0b1+a1b0)+
Δc(a0b1+a1b0)+ 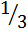 ΔaΔbΔc.
ΔaΔbΔc.
3) Четырехфакторная мультипликативная модель:
y = 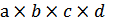
Δya= 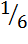 Δa[3b0c0d0+b1d0(c1+Δc)+d1c0(b1+Δb)+c1b0(d1+Δd)]+
Δa[3b0c0d0+b1d0(c1+Δc)+d1c0(b1+Δb)+c1b0(d1+Δd)]+ 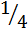 ΔaΔbΔcΔd;
ΔaΔbΔcΔd;
Δyb= 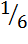 Δb[3a0c0d0+a1d0(c1+Δc)+d1c0(a1+Δa)+c1a0(d1+Δd)]+
Δb[3a0c0d0+a1d0(c1+Δc)+d1c0(a1+Δa)+c1a0(d1+Δd)]+ 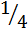 ΔaΔbΔcΔd;
ΔaΔbΔcΔd;
Δyc= 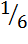 Δc[3a0b0d0+a1d0(b1+Δb)+d1b0(a1+Δa)+b1a0(d1+Δd)]+
Δc[3a0b0d0+a1d0(b1+Δb)+d1b0(a1+Δa)+b1a0(d1+Δd)]+ 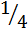 ΔaΔbΔcΔd;
ΔaΔbΔcΔd;
Δyd= 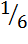 Δd[3a0b0c0+a1c0(b1+Δb)+c1b0(a1+Δa)+b1a0(c1+Δc)]+
Δd[3a0b0c0+a1c0(b1+Δb)+c1b0(a1+Δa)+b1a0(c1+Δc)]+ 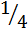 ΔaΔbΔcΔd.
ΔaΔbΔcΔd.
4) Кратная модель
y = 
Влияние факторов определяется по формулам:
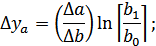
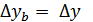 -
- 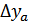 .
.
5) Смешанная трехфакторная модель
6) y = 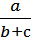
Влияние факторов определяется по формулам:
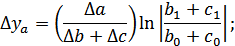
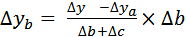 ;
;
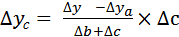 .
.
 2015-04-30
2015-04-30 320
320








