Функция распределения непрерывной случайной величины F (x) = P (X < x) является непрерывно дифференцируемой, за исключением конечного числа точек.
Все свойства функции распределения дискретной случайной величины выполняются и для функции распределения непрерывной случайной величины.
Производная от функции распределения F (x) называется плотностью распределения вероятностей (или дифференциальной функцией распределения):
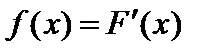 .
.
Пример 3.12. Дана функция распределения непрерывной случайной величины
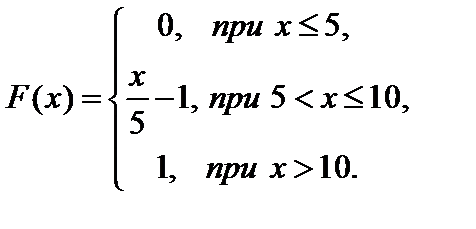
Найти плотность распределения этой случайной величины.
Решение
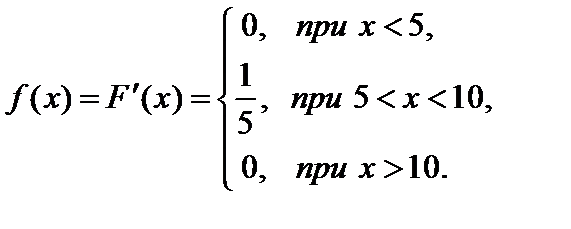
При x = 5 имеем: 
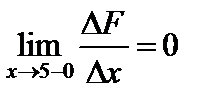 ,
, 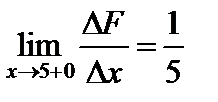 .
.
Так как 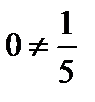 , то
, то 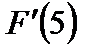 не существует.
не существует.
При x = 10 имеем: 
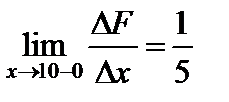 ,
, 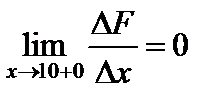 .
.
Так как 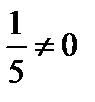 , то
, то 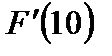 не существует.
не существует.
Тест 3.9. Дана функция распределения непрерывной случайной величины X:
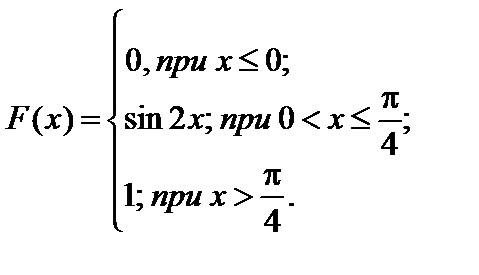
Дифференциальная функция распределения (плотность распределения) f (x) будет равна:
1) 0;
2) 1;
3) 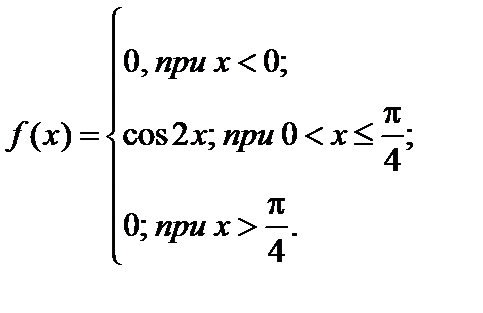
4) 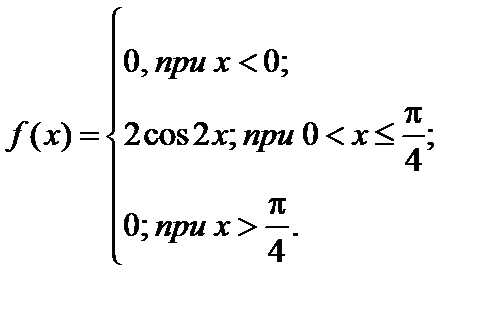
5) 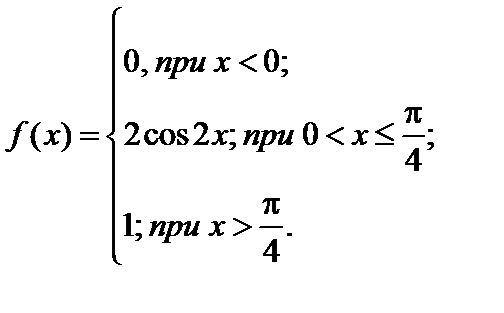
Зная плотность распределения, можно найти функцию распределения по формуле
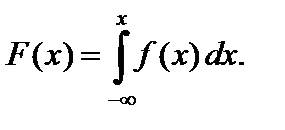
Вероятность того, что непрерывная случайная величина x примет значение, принадлежащее интервалу (a; b), определяется равенством
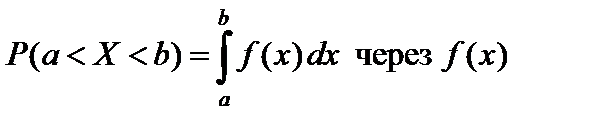 ,
,
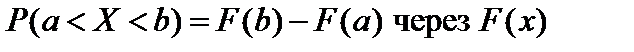 .
.
Пример 3.13. Дана функция распределения непрерывной случайной величины X
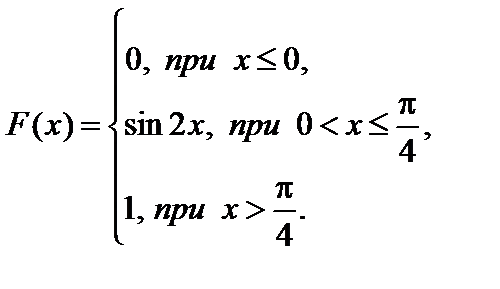
Найти вероятность того, что X примет значение, принадлежащее интервалу 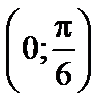 , через
, через 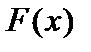 и
и 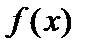 .
.
Решение
1. Воспользуемся формулой
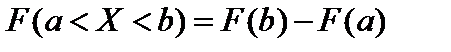 .
.
По условию 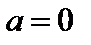 ;
; 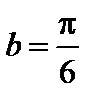 ; на этом интервале
; на этом интервале 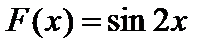 . Следовательно, искомая вероятность
. Следовательно, искомая вероятность
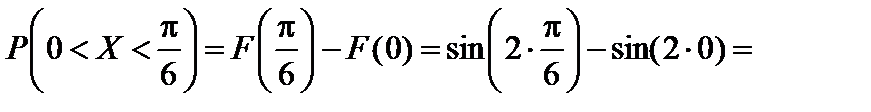
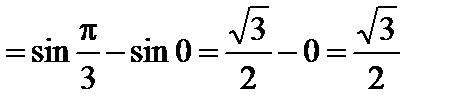 .
.
2. Найдем плотность распределения:
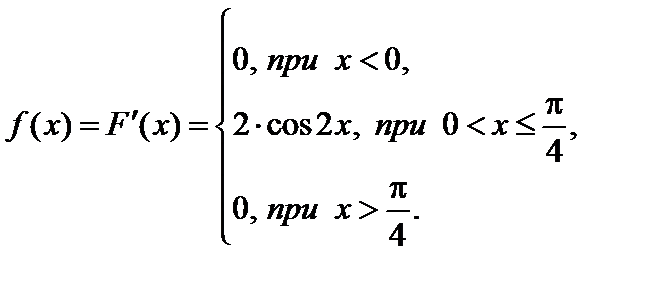
Воспользуемся формулой 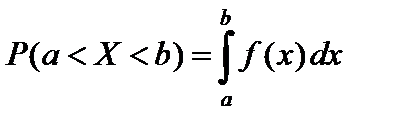 .
.
Тогда 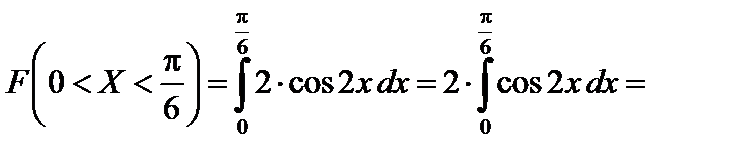
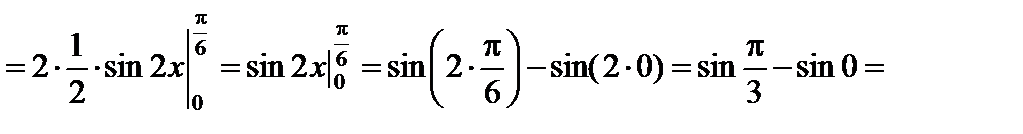
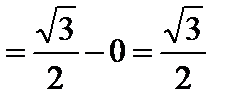 .
.
Ответ: 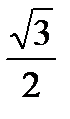 .
.
Тест 3.10. Дана функция распределения непрерывной случайной величины
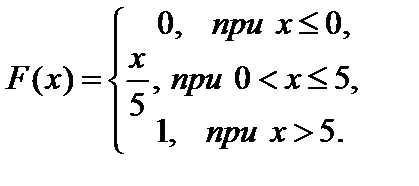
Вероятность того, что случайная величина примет значение, заключенное в интервале (3;4), равна:
1) 0;
2) 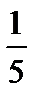 ;
;
3) 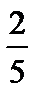
4) 1;
5) 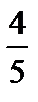 .
.
 2015-04-20
2015-04-20 2448
2448
