Случайная величина X, которая может принять возможное значение 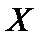 = k (k = 0; 1; …; n) с вероятностью, определяемой по формуле Бернулли
= k (k = 0; 1; …; n) с вероятностью, определяемой по формуле Бернулли
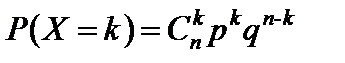 ,
,
называется распределенной по биномиальному закону.
Постоянные n и p (q = 1 – p) называются параметрами биномиального распределения.
Теорема. Числовые характеристики случайной величины,распределенной по биномиальному закону, вычисляются по формулам:
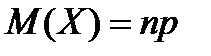 ;
; 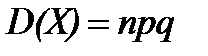 .
.
Таким образом, в примере 3.9 математическое ожидание и дисперсию можно было вычислять следующим образом:
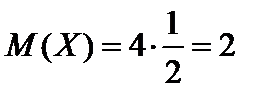 ;
; 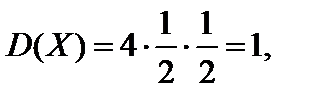
здесь n = 4; p = 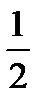 ; q =
; q = 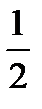 .
.
Тест 4.1. Монету бросают 4 раза. Случайная величина X – число выпадений герба. математическое ожидание случайной величины X равно:
1) 2;
2) 0;
3) 1;
4) 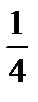 ;
;
5) 4.
Тест 4.2. Монету бросают 4 раза. Случайная величина X – число выпадений герба. Дисперсия случайной величины X равна:
1) 2;
2) 0;
3) 1;
4) 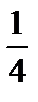 ;
;
5) 4.
Тест 4.3. Случайная величина X называется распределенной по биномиальному закону, если она принимает возможные значения с вероятностью, определяемой по формуле:
1) 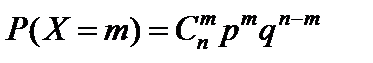 ;
;
2) 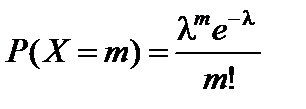 ;
;
3) 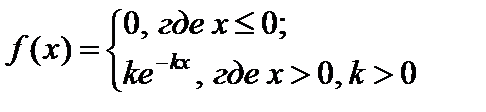 ;
;
4) 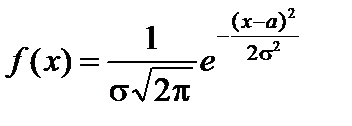 ;
;
5) 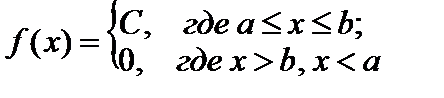 .
.
Тест 4.4. Математическое ожидание, дисперсия непрерывной случайной величины X, биномиально распределенной случайной величины равны:
1) 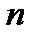 ;
; 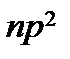 ;
;
2) 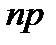 ,
, 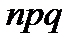 ;
;
3) 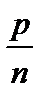 ;
; 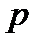 ;
;
4) 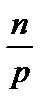 ;
; 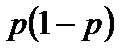 ;
;
5) 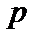 ,
, 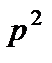 .
.
 2015-04-20
2015-04-20 1246
1246
