2015-04-20
2679
Наряду с уравнением (2.1) рассмотрим задачу
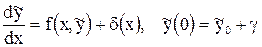, (2.2)
где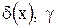 
- возмущения”, вносимые в правую часть уравнения (2.1) и начальные условия.
Задача Коши (2.1) абсолютно устойчива [4], если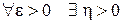 
такое, что 
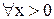из условия 
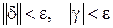следует 
.
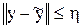Иначе говоря, решение устойчиво, если “возмущенное” решение “не слишком сильно” отличается от исходного.
Рассмотрим условия устойчивости решения по начальному условию, то есть положим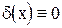 
.
Оценим погрешность решения
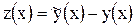. (2.3)
Для этого, вычитая уравнение (2.1) из выражения (2.2), получаем:
.
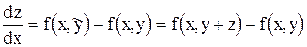Воспользовавшись теоремой Лагранжа о среднем, для правой части последнего выражения получим:
.
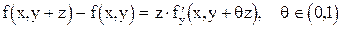Решаем полученное дифференциальное уравнение
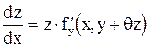
разделяя переменные:
,
,
,
.
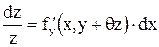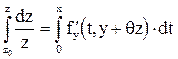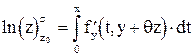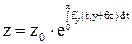Очевидно, что погрешность z(t) не будет возрастать, если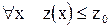 
. Но это возможно в том случае, когда 
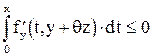. Поскольку это требование должно выполняться для любого значения x, необходимо потребовать, чтобы выполнялось условие 
.
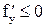Пример 2.1. Расмотрим задачу: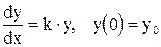 
.
Точное решение этого уравнения имеет вид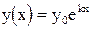 
. В случае k < 0 условие устойчивости выполняется:
|
|
|
,
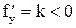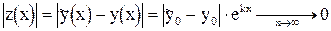
и различие между решениями уменьшается с увеличением значения аргумента (рис. 2.1а).
При k > 0 условие устойчивости не выполняется:
,
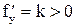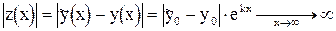
и различие между решениями увеличивается с ростом аргумента x (рис. 2.1б).
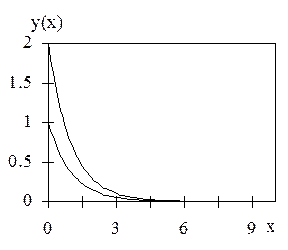
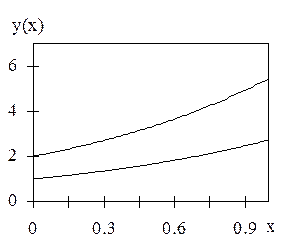
а б
Рис. 2.1. Примеры сходимости (а) и расходимости (б) решений действительного (нижние кривые) и возмущенного при начальных условиях (верхние кривые).
Метод Пикара [4]
Проинтегрируем уравнение (2.1) с помощью разделения переменных:
,
,
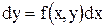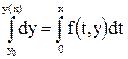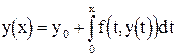. (2.4)
Используя последнее соотношение, построим итерационный процесс:
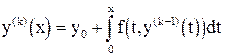, (2.5)
при этом в качестве “нулевого” приближения выбирается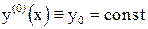 
.
Интеграл в правой части процедуры (2.4) вычисляется точно или численно.
Пример 2.2. Найдем методом Пикара решение уравнения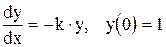 
.
Начальное приближение, в соответствии с идеей метода,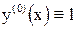 
.
Первое приближение:
.
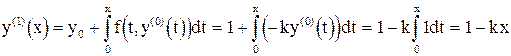Аналогично определяются второе
,
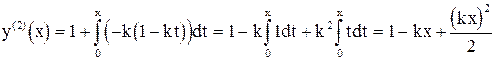третье
,
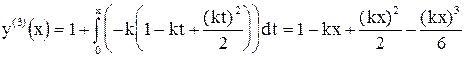четвертое
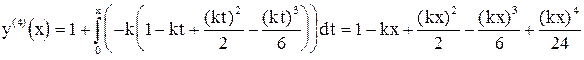
приближения, и так далее. Становится очевидным, что получаемая последовательность решений представляет собой частичные суммы разложения в ряд Тэйлора экспоненты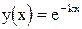 
, являющейся точным решением поставленной задачи.
Рассмотрим условия сходимости метода Пикара.
Пусть определена ограниченная область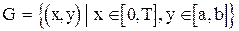 
, в которой правая часть 
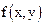уравнения (2.1) удовлетворяет условию Липшица
.
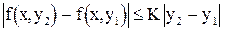Вследствие ограниченности области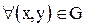 
выполнены соотношения:
.
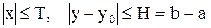Вычитая из соотношения (2.5) уравнение (2.4), определим погрешность приближенного решения:
.
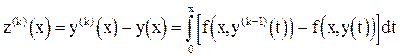Оценим модуль погрешности:
.
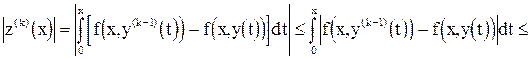
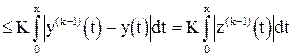Поскольку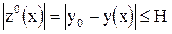 
(решение рассматривается внутри G), получаем:
,
,
,...,
.
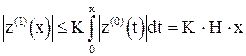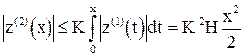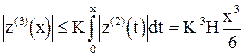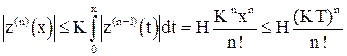В силу того, что
,
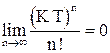приходим к заключению, что погрешность решения уменьшается с увеличением числа итераций:
|
|
|
,
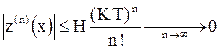то есть метод Пикара сходится к точному единственному решению исходной задачи.
