Профильный уровень
Вариант 1
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||

| 
| ||
| 
|
16.
Рассмотрим треугольники 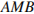 и
и 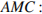 они прямоугольные, имеют общую сторону
они прямоугольные, имеют общую сторону 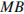 и равные стороны
и равные стороны 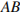 и
и 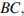 следовательно, эти треугольники равны по двум катетам, значит,
следовательно, эти треугольники равны по двум катетам, значит, 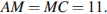 Рассмотрим треугольник
Рассмотрим треугольник 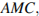 воспользовавшись теоремой косинусов найдём косинус угла
воспользовавшись теоремой косинусов найдём косинус угла 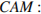
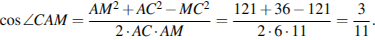
Из треугольника 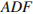 найдём сторону
найдём сторону 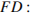
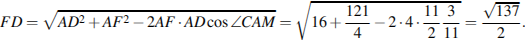
Рассмотрим прямоугольный треугольник 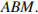 Найдём косинус угла
Найдём косинус угла 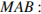
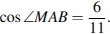
Из треугольника 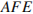 найдём сторону
найдём сторону 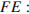
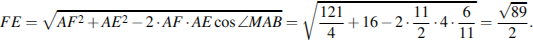
В треугольнике 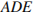
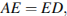 следовательно, он равнобедренный, углы при основании равны. Угол
следовательно, он равнобедренный, углы при основании равны. Угол 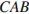 равен 60°, значит,
равен 60°, значит, 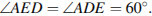 Следовательно, треугольник
Следовательно, треугольник 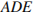 — равносторонний,
— равносторонний, 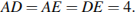
Найдём косинус угла 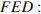
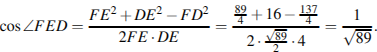
Следовательно, 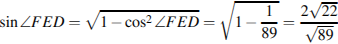
Треугольник 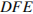 — искомое сечение, найдём его площадь:
— искомое сечение, найдём его площадь:
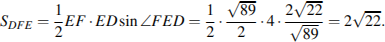
Ответ: 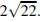
21.
1. Сразу заметим, что уравнение имеет единственный корень 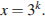 Следовательно, формула общего члена последовательности имеет вид
Следовательно, формула общего члена последовательности имеет вид 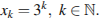
Для ответа на первый вопрос заметим, что 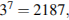 тогда число
тогда число 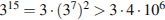 содержит в десятичной записи более семи цифр. Легко убедитьcя, что условию задачи удовлетворяет число
содержит в десятичной записи более семи цифр. Легко убедитьcя, что условию задачи удовлетворяет число 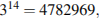 то есть
то есть 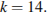
2. Число будет содержать среди делителей ровно 8 членов данной последовательности в случае, если его делителями являются первые 8 членов последовательности, а девятый уже не является. Следовательно, искомое натуральное число должно делиться на 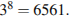 Для того, чтобы оно было наименьшим, оно не должно иметь других делителей, то есть это число 6561.
Для того, чтобы оно было наименьшим, оно не должно иметь других делителей, то есть это число 6561.
3. Нет. Предположим, что такой набор существует, то есть при некоторых значениях 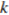 и
и 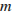 имеет место равенство
имеет место равенство 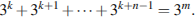
По формуле суммы геометрической прогрессии со знаменателем 3 свернем левую часть последнего равенства. Тогда получаем равенство 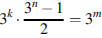 или
или 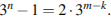 Отсюда получаем равенство
Отсюда получаем равенство 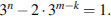 Последнее равенство возможно только при выполнении условий
Последнее равенство возможно только при выполнении условий 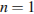 и
и 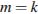 (иначе правая часть равна 1, а левая делится на 3), что не удовлетворяет условию задачи.
(иначе правая часть равна 1, а левая делится на 3), что не удовлетворяет условию задачи.
4. Да, существует. Этому условию удовлетворяет любой набор, содержащий 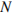 членов (в том числе и 2012 членов) последовательности, каждый из которых имеет вид
членов (в том числе и 2012 членов) последовательности, каждый из которых имеет вид 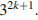 Тогда любой набор содержит минимальное число, которое при суммировании можно вынести за скобки и получится выражение вида
Тогда любой набор содержит минимальное число, которое при суммировании можно вынести за скобки и получится выражение вида 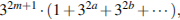 которое не является квадратом.
которое не является квадратом.
Профильный уровень
Вариант 2
| 
| ||

| 
| ||
| |||
| 
| ||
| 
| ||
| |||

| 
|
21.
Решение.
а) Ясно, что количество треугольников не может быть больше числа сочетаний из восьми по три, а 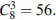
б) Пусть длины отрезков такие: 20, 19, 18, 17, 16, 15, 14, 6. Тогда возможно ровно 55 треугольников (из 56 возможных сочетаний не годится только одно: 6, 14, 20. Для всех остальных неравенство треугольника выполнено).
в) Докажем, что  не годится. Пусть длины отрезков равны
не годится. Пусть длины отрезков равны 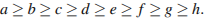 Если ни одного треугольника составить нельзя, то
Если ни одного треугольника составить нельзя, то 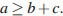 Аналогично,
Аналогично, 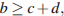 значит
значит 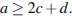 Тогда
Тогда 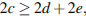 значит,
значит, 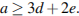 Продолжая цепочку, получим:
Продолжая цепочку, получим: 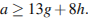 Значит,
Значит,  не меньше 21. Противоречие.
не меньше 21. Противоречие.
Приведем пример с 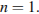 Используя предыдущее рассуждение получаем такой набор:
Используя предыдущее рассуждение получаем такой набор:
1, 1, 2, 3, 5, 8, 13, 20. Единственный возможный треугольник — это 8, 13, 20.
Ответ: а) Нет; б) Да; в) 1.
 2015-04-30
2015-04-30 148
148







