Как уже отмечалось выше, одним из наиболее обширных и изученных разделов математического программирования является раздел линейного программирования, где как целевая функция математической модели, так и все ограничения в системе ограничений являются линейными относительно входящих в них переменных функциями.
В предыдущем разделе были рассмотрены содержательные постановки ряда экономических задач, математические модели которых имеют линейную структуру, т.е. относятся к классу задач линейного программирования (ЗЛП). Естественно, что этим задачи ЛП себя не исчерпали. Существует огромное количество ЗЛП с различными словесными формулировками. Но, несмотря на различие содержательных ситуаций ряда задач ЛП, экстремальные математические модели, соответствующие им, имеют много общего. Так, в каждой из этих задач требуется максимизировать или минимизировать линейную функцию от нескольких переменных. При этом ограничения, наложенные на совокупность переменных, являются либо линейными уравнениями, либо линейными неравенствами, либо состоят как из линейных уравнений, так и из линейных неравенств. Каждая из этих задач является частным случаем общей задачи ЛП.
Общей задачей ЛП называется задача, которая состоит в определении максимального (минимального) значения функции:
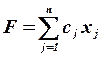 (3.1)
(3.1)
при условиях:
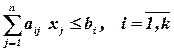 (3.2)
(3.2)
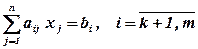 (3.3)
(3.3)
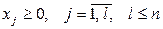 (3.4)
(3.4)
где aij, bi, cj - заданные постоянные величины и k £ m.
Функция (3.1) называется целевой функцией задачи (3.1) – (3.4), а условия (3.2) – (3.4) – ограничениями данной задачи.
Различают еще две основные формы задач ЛП в зависимости от наличия ограничений разного типа: стандартную и каноническую.
Стандартной (или симметричной) ЗЛП называется задача, которая состоит в определении максимального значения функции (3.1) при выполнении условий (3.2) и (3.4), где k = m, и l = n, т.е.
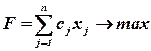
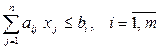 (3.5)
(3.5)
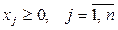
Канонической (или основной) ЗЛП называется задача, которая состоит в определении максимального значения целевой функции (3.1) при выполнении условий (3.3) и (3.4), где k=0, и l=n, т.е.
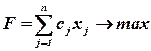
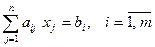 (3.6)
(3.6)
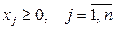
Стандартная форма модели интересна тем, что большое число прикладных моделей естественным образом сводится к этому виду моделей. Каноническая форма модели важна ввиду того, что основные вычислительные схемы различных алгоритмов решения этих задач разработаны именно для этой формы.
Указанные выше три формы ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть приведена к любой из двух остальных. Следовательно, любую ЗЛП можно привести к канонической форме. Поэтому умение решать задачу в канонической форме позволяет решать задачу и в любой другой форме.
Чтобы перейти от одной формы записи ЗЛП к другой нужно уметь:
1) сводить задачу минимизации функции к задаче максимизации;
2) переходить от ограничений – неравенств к ограничениям – равенствам;
3) заменять переменные, которые не подчинены условию неотрицательности, на неотрицательные переменные.
1. В том случае, когда требуется найти min функции F = c1x1 + c2x2 +…+ cnxn, можно перейти к нахождению максимума функции F1, умножив коэффициенты при переменных в целевой функции модели на (-1), т.е.:
F1 = - F = - c1x1 - c2x2 - ……- cnxn, т.к. min F = - max (- F).
2. Ограничение – неравенство исходной задачи ЛП можно преобразовать в ограничение – равенство добавлением к его левой части неотрицательной переменной с соответствующим знаком.
Таким образом, ограничение – неравенство вида
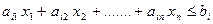
преобразуется в ограничение – равенство
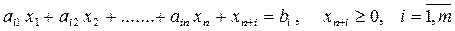 ,
,
а ограничение – неравенство вида
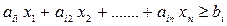
в ограничение – равенство
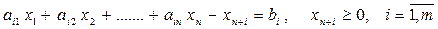 .
.
Число вводимых дополнительных неотрицательных переменных при подобных преобразованиях равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи ЛП отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной следует интерпретировать как остаток, или неиспользованную часть, данного ресурса.
3. Если переменная Хк не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными 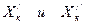 , приняв
, приняв 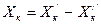 . Правомерность такой замены очевидна, т.к. любое число можно представить в виде разности двух неотрицательных чисел.
. Правомерность такой замены очевидна, т.к. любое число можно представить в виде разности двух неотрицательных чисел.
 2015-04-30
2015-04-30 3426
3426
