Математическая постановка задачи

Обозначим через х₁ (га) площадь, которая отводится под рожь на первом массиве, через х ₂ (га) площадь, которая отводится под рожь на втором массиве, через х ₃ (га) площадь, которая отводится под рожь на третьем массиве.

Аналогично через х ₄, х ₅, х ₆ (га) обозначим соответственно площадь под пшеницу на первом, втором и третьем массивах и через х ₇, х ₈, х₉ (га) — площадь под кукурузу на первом, втором и третьем массивах.

Составим систему уравнений:

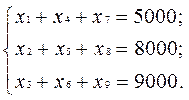
Учитывая урожайность каждой культуры на каждом с массивов, и взяв во внимание план, получим такие три ограничения:

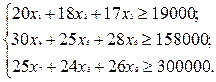
Целевая функция задачи, выражающая суммарную прибыль сельскохозяйственного предприятия от реализации урожая, имеет вид:

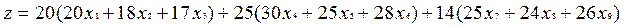
Необходимо найти такие положительные значения х ₁, х ₂,.., х ₉, которые удовлетворяют уравнениям и неравенствам системы и доставляют целевой функции максимум.

Методами математического программирования решаются кроме рассмотренных и многие другие задачи, например, задачи о назначении, военные задачи, задачи о рациональном использовании отходов химического производства и т.п.

Все эти задачи решаются по одной и той же схеме: имеется некоторое количество чего-либо, например, количество изделий, известна их стоимость, прибыль, себестоимость и/или другие показатели эффективности функционирования изучаемого объекта, которые выражаются линейной (или нелинейной) функцией ряда переменных. Эти переменные в свою очередь удовлетворяют ограничениям, указанным в системах линейных (либо нелинейных) неравенств и/или уравнений. Требуется узнать такое неотрицательное решение системы ограничений, при котором целевая функция принимает наименьшее либо наибольшее значение (в зависимости от цели, поставленной в задачи).