2015-04-30
1415
В ЛП сложилась определенная терминология, которой мы и будем придерживаться.
Совокупность чисел – вектор Х = (х1, х2, ….., хn), удовлетворяющих ограничениям задачи (3.2) – (3.4), называется допустимым решением.
Допустимое решение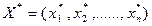 
, при котором целевая функция задачи (3.1) принимает свое максимальное (минимальное) значение, называется оптимальным решением.
Запишем задачу ЛП, представленную в канонической форме, в векторной форме:
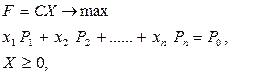(3.7)
где С = (с1, с2,…,сn), Х = (х1, х2…,хn), СХ - скалярное произведение векторов, Р1,…..Рn, Ро – m -мерные вектор – столбцы, составленные из коэффициентов при неизвестных и свободных членов системы уравнений задачи:
.
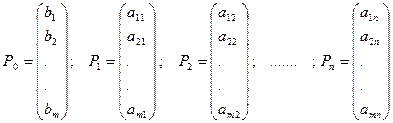Решение Х = (х1, х2,…..хn) канонической задачи (3.7) называется опорным планом, если система векторов Pj, соответствующих положительным компонентам Xj, линейно независима.
Так как векторы Рj являются m – мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше чем m. Остальные его (n-m) компонент равны нулю.
Опорный план называется невырожденным, если он содержит ровно m положительных компонент, в противном случае он называется вырожденным.
Свойства основной задачи ЛП (3.7) тесным образом связаны со свойствами выпуклых множеств.
Пусть Х1, Х2,…..Хn - произвольные точки евклидова пространства En. Выпуклой линейной комбинацией этих точек называется сумма
a1 х1 + a2 х2 + …… + an xn,
где ai – произвольные неотрицательные числа, сумма которых равна 1:
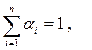a i ³ 0,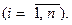 
Точка Х выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества.
Свойства основной задачи ЛП
Теорема 3.1 Множество планов основной задачи ЛП является выпуклым (если оно не пусто).
Непустое множество планов основной задачи ЛП называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.
Теорема 3.2 Если основная задача ЛП имеет оптимальный план, то максимальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное значение целевая функция принимает в более, чем одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.
Теорема 3.3 Если система векторов Р1, Р2,…..Рk, (k £ n) в разложении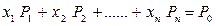 
линейно независима и такова, что 
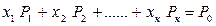, где все хi ³0, то точка Х =(х1, х2,…..хк,, 0,…., 0) является вершиной многогранника решений.
Теорема 3.4 Если Х = (х1, х2,…..хn) – вершина многогранника решений, то векторы Рj, соответствующие положительным xj в разложении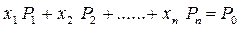 
, линейно независимы.
Геометрическая интерпретация ЗЛП
Сформулированные теоремы позволяют сделать следующие выводы.
Непустое множество планов основной задачи ЛП образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т.е. для одного из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Если максимальные значения функция принимает более, чем в одной вершине, то это значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.
Геометрическая интерпретация ЗЛП позволяет разработать и в некоторых случаях использовать (в случае, когда n-m =2, где n – количество переменных в задаче, m – число линейно независимых ограничений в системе ограничений ЗЛП) несложный метод ее решения – графический метод.
