2015-04-30
1093
1. Основные двойственные переменные показывают, на сколько изменится целевая функция прямой задачи при изменении соответствующего ресурса на единицу. Как следует из теоремы 3.6 (Fmax =Lmin), двойственная переменная численно равна вкладу в целевую функцию изменения соответствующего ограниченного ресурса на единицу.
Пусть, например, i й ресурс увеличили на единицу, т.е. b/i=bi +1. Тогда оптимальное значение целевой функции двойственной задачи также изменится:
.
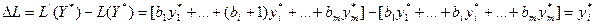Учитывая условие теоремы 3.6, приходим к выводу, что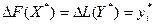 
, т.е. если i й ресурс является дефицитным (
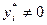), то его увеличение приведет к пропорциональному росту значения целевой функции Fmax. Данное свойство оптимальных двойственных оценок позволяет выявлять направления мероприятий по устранению «узких» мест, обеспечивающих наибольший экономический эффект.
2. Дополнительные двойственные переменные свидетельствуют о том, на сколько внутренние оценки ресурсов (левая часть ограничений), необходимых для производства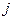 
-го вида продукции, превосходят его внешнюю оценку, т.е. цену продукции 
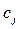. Для продукции (или технологии), которая вошла в оптимальный план, их дополнительные двойственные переменные равны нулю. Их внедрение в производство не несет убытка. Если же некоторая продукция не вошла в оптимальный план, то изготовление такой продукции даст убыток. Возможный убыток равен значению дополнительной двойственной переменной.
|
|
|
3. Состав двойственной переменной. Пусть, например, первый ресурс дефицитный. Ему соответствует дополнительная переменная прямой задачи Xn+1. Данной переменной соответствует столбец Рn+1. в оптимальной симплекс-таблице: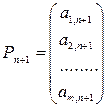 
. Если теперь первый ресурс изменить на единицу, а 
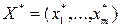- вектор значений оптимальных базисных переменных, то базисные переменные в оптимальном плане изменятся по формулам: 
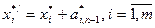. Пусть, например, в задаче об использования сырья (пример 2.1) первый ресурс (продукт А) увеличили на 1 тонну. Соответствующая данному ресурсу дополнительная переменная прямой задачи (х*3) представлена в оптимальной симплекс-таблице (см. пример 3.10) столбцом 
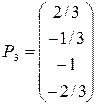. Поэтому новые значения базисных переменных оптимального плана задачи изменятся по формулам:
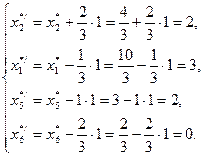
При этом изменяется и значение целевой функции задачи:
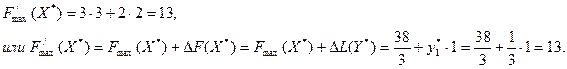
Необходимо иметь в виду, что двойственные оценки позволяют судить об эффекте не любых, а лишь сравнительно небольших изменений объема ресурсов. При резких изменениях может поменяться структура оптимального плана задачи, а следовательно, и сами оценки могут стать другими.
4. Взаимозаменяемость ресурсов. Возникает естественный вопрос: если первый и второй ресурсы дефицитны и, например, первый уменьшился на единицу, то на сколько единиц нужно увеличить второй ресурс, чтобы экстремальное значение целевой функции не изменилось? Введем понятие коэффициента взаимозаменяемости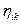 
.
|
|
|
Коэффициент 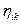показывает, сколько единиц ресурса 
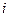необходимо дополнительно иметь, чтобы компенсировать уменьшение ресурса 
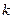на единицу при неизменном значении целевой функции. Его рассчитывают по формуле: 
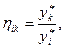где 
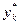и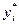 
- двойственные оценки в оптимальном плане 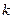-го и 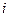-го ресурсов соответственно.
Для задачи об использовании сырья значения коэффициентов взаимозаменяемости представлены в таблице:
| ||||
| 1 | 4 | 0 | 0 | |
| 1/4 | 1 | 0 | 0 | |
|
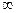
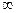
| 1 | 0 | |
|
|
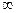
| 0 | 1 |
Например, для рассчитаем коэффициент взаимозаменяемости второго ресурса первым: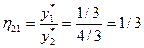 
, т.е. при уменьшении суточного запаса продукта А на 1 тонну необходимо дополнительно увеличить суточный запас продукта В на 1/3 тонны чтобы значение целевой функции не изменилось. Как показывают расчеты значений коэффициентов взаимозаменяемости для рассматриваемого примера его значение больше 1, если более дефицитный ресурс заменяется менее дефицитным, и меньше 1, если происходит обратная замена. Знак «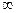» означает, что заменить уменьшение дефицитного ресурса недефицитным не возможно, а «0» означает, что при уменьшении недефицитного ресурса не требуется дополнительное увеличение дефицитного ресурса.
5. Оценка новых технологий (продукции) с позиции общего оптимума. В оптимальный план задачи на получение максимума прибыли может быть включен лишь тот вид продукции (способ производства), для которого прибыль недополученная из-за отвлечения дефицитных ресурсов, покрывается полученной прибылью от его реализации cj. Разность между недополученной и полученной прибылью служит характеристикой рентабельности данной продукции (способа производства).
Пусть в рассматриваемом примере фирма разработала новый вид продукции – краску для наружных работ К. Апробация его позволила определить расход каждого ограниченного ресурса на 1 тонну краски: по ¾ тонны продуктов А и В, а проведенные маркетинговые исследования показали, что цена за 1 тонну данной краски должна составлять 1,5 тыс. грн. Требуется выяснить целесообразность внедрения в серийное производства краски К, т.е. обеспечит ли ее выпуск увеличение целевой функции (дохода от реализации). Обозначим через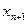 
планируемый объем производства краски К. Как отмечалось выше, каждой основной переменной прямой задачи соответствует ограничение двойственной. Если 
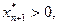то соответствующее ему ограничение выполняется как строгое равенство (теорема 3.2):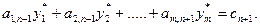 
В этом случае новый вид продукции (новая технология) рентабелен. Если же дополнительное ограничение имеет вид: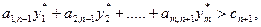 
то значение дополнительной двойственной переменной 
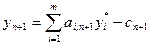покажет, на сколько уменьшится значение целевой функции при производстве единицы продукции нового вида (при использовании новой технологии в единицу времени).
Таким образом, показателем рентабельности (оправданности по затратам) нового вида продукции является величина: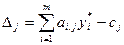 
, где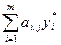 
- суммарные затраты на производство единицы продукции j -го вида, измеренные во внутренних ценах (двойственных оценках), 
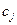- внешняя оценка единицы продукции j -го вида (например, ее цена). Если 
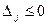, внедрение в производство продукции j -го вида оправдано по затратам дефицитных ресурсов, если 
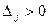, производство не выгодно. Причем равенство нулю (
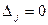) позволяет определить минимальное (граничное) значение внешней оценки продукции j -го вида, при которой ее производство будет рентабельно.
Примечание. В случае, когда прямая задача решается на минимум, значение показателя рентабельности берется в обратном порядке к описанной выше ситуации, т.е. рентабельно, если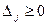 
.
|
|
|
Экономико-математический послеоптимизационный анализ позволяет дополнительно получить ценную информацию, дающую возможность более обосновано принимать управленческие решения.
4. специальные задачи Линейного программирования: сети
Многие задачи, возникающие как в экономике, так и в других сферах общественной деятельности, могут быть математически описаны как задачи линейного программирования. Для задач, поддающихся такому описанию, существует унифицированный алгоритм решения – симплексный метод.
Однако достаточно большое количество задач линейного программирования при решении их симплексным методом требует наличия существенных вычислительных мощностей, что не оправдывает применение данного метода решения.
Множество таких задач могут быть описаны и решены более рационально в рамках специальных теорий, которые разрабатывают эффективные алгоритмы решения задач, объединенных в некоторые классы однотипных задач. Так существует ряд задач, которые удобно представлять, например, в виде графических структур (сетей). Например, можно формализовать процесс принятия решения, функционирование производственной системы, транспортировку продукции, передачу информации и т.д.
Перечисленные задачи можно сформулировать и решить как задачи линейного программирования. Однако из-за огромного числа переменных и ограничений в сетевых задачах непосредственное применение симплекс-метода нецелесообразно. Специальная структура этих задач позволяет разработать более эффективные алгоритмы их решения.
Рассмотрим более подробно типичные примеры специальных ЗЛП и методы их решения, а именно: транспортную задачу и модификации ее постановки на сетевых моделях (графах).
