Ограничения на допустимое множество. Выпуклые множества

Ограничения вида (5.1) являются наиболее типичным способом задания допустимого множества 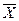. При некоторых видах ограничений допустимое множество может оказаться пустым (рис. 5.1.). В этом случае ограничения

x ₁ x ₂ >1

x ₁²+ x ₂² 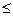1

будут называться несовместимыми.

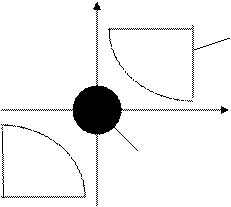x ₂

х ₁ х ₂>1

x ₁

x ₁²+ x ₂² 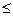1

Рис. 5.1. Пустое множество

Рассмотренные далее методы оптимизации применимы в том случае, если допустимое множество является выпуклым.

Определение 5.3. Множество точек 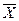называется выпуклым, если вместе с любыми двумя его точками ему принадлежит и отрезок, соединяющий эти точки.

Определение 5.4. Отрезком, соединяющим две точк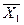и и 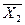, называется множество точек 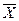, удовлетворяющих уравнению 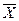= t 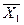+(1- t) 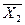, где 0< t <1.

Теорема 5.1. Пересечение выпуклых множеств есть выпуклое множество.

На рис. 5.2. показаны примеры выпуклого (рис. 5.2а) и невыпуклого (рис. 5.2б) множеств.

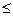х ₁²+ х ₂²£1 х ₁²+ х ₂² 1

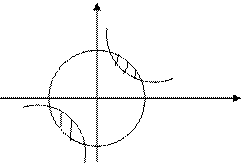
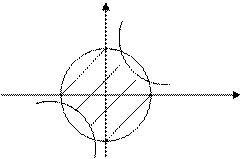x ₂ х ₁ х ₂³1 x ₂ x ₁ x _2<1

0 x ₁ 0 x ₁

а) б)

Рис. 5.2. Множества: выпуклое а); невыпуклое б).