Метод линеаризации – один из наиболее эффективных методов решения задач математического программирования. Данный метод базируется на идее линейной или квадратичной аппроксимации целевой функции в окрестностях очередной точки. Поэтому в качестве вспомогательных возникают задачи линейного или квадратичного программирования.
Общая постановка задачи:
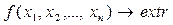 (5.45)
(5.45)
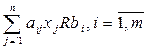 (5.46)
(5.46)
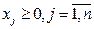
Здесь R – отношения вида 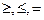 .
.
Суть метода при линейной аппроксимации заключается в том, что:
1. Нелинейная функция (5.45) заменяется линейной в точке 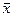 (к), принадлежащей допустимой области G
(к), принадлежащей допустимой области G
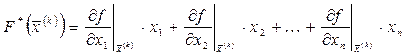 (5.47)
(5.47)
2. Решается задача линейного программирования:
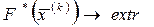 (5.48)
(5.48)
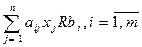
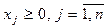
Пусть решением этой задачи является точка 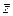 (k).
(k).
3. Из точки 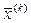 в направлении
в направлении 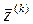 смещаемся с некоторым шагом
смещаемся с некоторым шагом 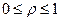 в точку
в точку 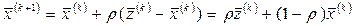 (5.49)
(5.49)
Так как 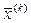 и
и 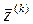 принадлежат допустимой области G, а область G, определяемая ограничениями (5.46) выпукла и
принадлежат допустимой области G, а область G, определяемая ограничениями (5.46) выпукла и 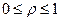 , то
, то 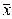 (k + 1)
(k + 1) 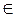 G.
G.
Шаг 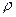 можно выбирать по-разному:
можно выбирать по-разному:
1) шаг 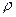 - произвольное, достаточно малое число
- произвольное, достаточно малое число 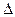 ;
;
2) шаг 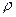 выбирается таким, при котором функция
выбирается таким, при котором функция 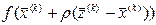 принимает наибольшее значение при всех
принимает наибольшее значение при всех 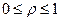 . Если найденное значение
. Если найденное значение 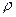 принадлежит концам отрезка [0;1], то необходимо выбрать один из концов этого отрезка.
принадлежит концам отрезка [0;1], то необходимо выбрать один из концов этого отрезка.
3. Итерации продолжаются до тех пор, пока
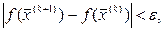 (5.50)
(5.50)
где 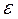 -положительное, малое число.
-положительное, малое число.
Пример 5.2 Требуется максимизировать функцию
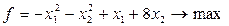 (5.51)
(5.51)
при условиях 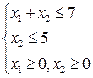 (5.52)
(5.52)
с точностью 0,1.
В качестве начального допустимого вектора берем 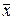 (0) = (0,0). Значение целевой функции в этой точке F (0) = 0. Нелинейную функцию (5.51) заменяем линейной и F * (0,0) в соответствии с (5.47)
(0) = (0,0). Значение целевой функции в этой точке F (0) = 0. Нелинейную функцию (5.51) заменяем линейной и F * (0,0) в соответствии с (5.47)
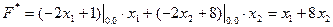
Далее решаем задачу: х1 + 8х2 ® mах
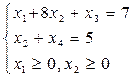
Здесь ограничения (5.52) приведены к каноническому виду.
| БП | Cб | В | ||||
| X1 | X2 | X3 | X4 | |||
| X1 | ||||||
| X4 | ||||||
| -1 | ||||||
| X1 | -1 | |||||
| X2 | ||||||
| -1 | -7 |
Итак, 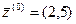 . Вектор
. Вектор 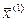 находим по формуле (5.49):
находим по формуле (5.49): 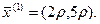 Шаг
Шаг 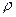 найдем из условия максимума f (
найдем из условия максимума f (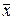 (1) ) при
(1) ) при 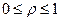 .
.
F (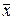 (1)) = - (2
(1)) = - (2 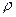 )2- (5
)2- (5 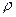 ) 2 + 2
) 2 + 2 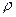 + 8*5
+ 8*5 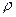 = -29
= -29 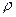 2 + 42
2 + 42 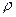 .
.
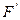 (
(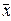 (1)) = - 58 + 42 = 0. Откуда
(1)) = - 58 + 42 = 0. Откуда 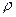 = 0,724.
= 0,724.
Следовательно 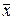 (1) = (1,448; 3,62). Значение целевой функции в этой точке F (1) = 15,207.
(1) = (1,448; 3,62). Значение целевой функции в этой точке F (1) = 15,207.
Вторая итерация: F * (1,448; 3,62) = -1,896 х 1 + 0,76 х 2; 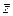 (1) = (0,5);
(1) = (0,5);
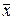 (2) = ((1-
(2) = ((1- 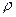 ) 1,448; 5
) 1,448; 5 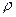 + (1-
+ (1- 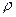 ) 3,62);
) 3,62); 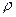 = 0,474;
= 0,474;
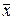 (2) = (0,762; 4,27); F (2) = 16,108.
(2) = (0,762; 4,27); F (2) = 16,108.
Третья итерация: F * (0,762; 4,27) = -0,524 х 1-0,54 х 2; 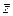 (2) = (0,0);
(2) = (0,0);
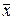 (3) = ((1-
(3) = ((1- 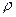 ) 0,762; (1-
) 0,762; (1- 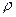 ) 4,27);
) 4,27); 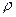 = 0,072;
= 0,072;
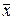 (3) = (0,707; 3,963); F (3) = 16,206.
(3) = (0,707; 3,963); F (3) = 16,206.
| F (3) - F (2) | = | 16,206-16,108 | = 0,098 < 0,1. То есть приближенно можно считать, что Fмax = 16,206; 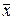 opt = (0,707; 3,963).Точное решение этой задачи: Fмax = 16,25;
opt = (0,707; 3,963).Точное решение этой задачи: Fмax = 16,25; 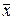 opt = (0,5; 4).
opt = (0,5; 4).
 2015-04-30
2015-04-30 2890
2890








