Краткая теория:
Наиболее распространенным подходом к численному вычислению интеграла является разбиение отрезка [a, b] на n равных частей а = х0 < х1<... < хn = b c шагом h, интерполирование функции y =f(x) на отрезке [a,b] и замена интеграла интегральной суммой:
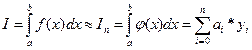 ,
,
где ai ¾ числовые коэффициенты.
В простейших случаях в качестве интерполяционного многочлена φ(x) берут ступенчатую, кусочно-линейную или кусочно-параболическую функции и др.
Для вычисления значения интегралов используют формулы:
- формула прямоугольников:
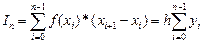 - по левым точкам
- по левым точкам
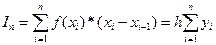 - по правым точкам
- по правым точкам
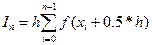 - по средним точкам
- по средним точкам
- формула трапеций:
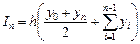
- формула Симпсона (n - четное число):
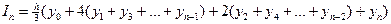
Решение задачи:
Найти интеграл функции, полученной в п.3, на отрезке [0,8] методом трапеций. Оценить погрешность.
Решение:
а) По условию задачи:
| хi | y |
| -4.4 | |
| 4.6 | |
| -1.7 | |
| -10 |
Тогда по методу трапеций можно получить значение интеграла:
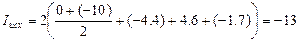
б) Метод трапеций по интерполяционному многочлену Лагранжа:
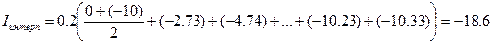 в) Метод трапеций по аппроксимации методом наименьших квадратов:
в) Метод трапеций по аппроксимации методом наименьших квадратов:
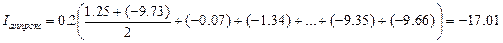
Аналогично п.5, если из условия задачи следует, что за реальное поведение системы можно принять поведение системы, описываемое с помощью аппроксимирующей функции (см. п.4), то реальное значение интеграла функции на данном отрезке можно рассчитать как интеграл аппроксимирующей функции на данном отрезке:
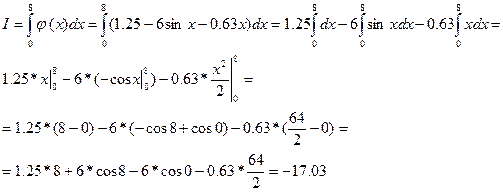
Вычисление погрешности:
а) 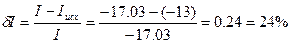
б) 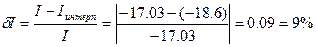
в) 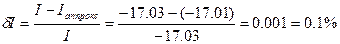
 2015-04-30
2015-04-30 388
388








