Для электрического поля получали формулу:
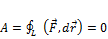 (1), или то же самое:
(1), или то же самое:
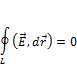
(работа сил электрического поля по замкнутому контуру равна нулю). Таким образом, доказывали, что электрическое поле – это поле консервативных сил, то есть, оно потенциально, из (1): 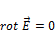 . Вывод: электростатическое поле – безвихревое.
. Вывод: электростатическое поле – безвихревое.
Наша задача: вычислить, чему равен 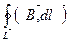 , посмотреть, потенциально ли магнитное поле. Если
, посмотреть, потенциально ли магнитное поле. Если 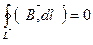 , то поле потенциально, если нет, то
, то поле потенциально, если нет, то 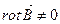 .
. 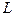 – это не проводник с током, а просто любой контур в магнитном поле с индукцией
– это не проводник с током, а просто любой контур в магнитном поле с индукцией 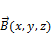 . В общем случае эта задача очень сложная, поэтому рассмотрим частный случай.
. В общем случае эта задача очень сложная, поэтому рассмотрим частный случай.
Мы уже находили, что магнитная индукция кругового тока равна: 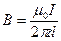
Выберем контур 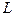 по силовой линии (окружность с радиусом
по силовой линии (окружность с радиусом 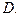 ). Вектор
). Вектор 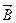 перпендикулярен вектору
перпендикулярен вектору 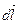 .
.

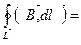
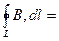

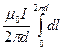 =
= 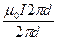 =
= 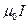
Для контура диаметром 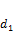 получим то же самое:
получим то же самое: 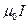 . Можно показать, что этот результат справедлив для контура любой формы и не обязательно плоского, таким образом
. Можно показать, что этот результат справедлив для контура любой формы и не обязательно плоского, таким образом 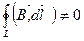 ,
,  то есть магнитное поле не потенциально. Оно вихревое, так как
то есть магнитное поле не потенциально. Оно вихревое, так как 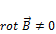 .
.
Если контур охватывает несколько токов, то:
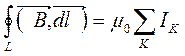
Токи, входящие в контур, беруться со знаком +, токи, выходящие из контура, со знаком -
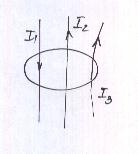
(Это не обязательно все проводники с током, это может быть, например, поток электронов в осциллографе). Если контур токов не охватывает, то 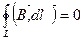 . Чтобы учесть все токи, проводят построение: строят произвольную поверхность, S, опирающуюся на контур
. Чтобы учесть все токи, проводят построение: строят произвольную поверхность, S, опирающуюся на контур 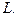 Рис.16.
Рис.16.
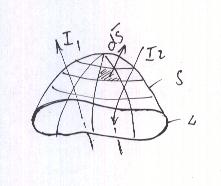
Рис. 16
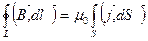
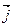 –плотность тока в каждой точке поверхности S.
–плотность тока в каждой точке поверхности S.
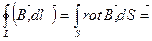
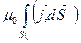 отсюда:
отсюда:
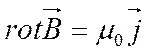 – магнитное поле имеет вихревой характер. Последние уравнение называется дифференциальной формой закона полного тока. Вспомним, что
– магнитное поле имеет вихревой характер. Последние уравнение называется дифференциальной формой закона полного тока. Вспомним, что 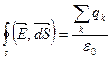 , откуда получапи:
, откуда получапи: 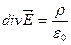 (источник электростатического поля). В природе магнитных зарядов не существует, поэтому поток вектора
(источник электростатического поля). В природе магнитных зарядов не существует, поэтому поток вектора 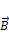 через замкнутую поверхность
через замкнутую поверхность 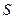
 равен нулю.
равен нулю.
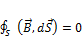 ,
, 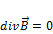
 2015-04-20
2015-04-20 563
563








