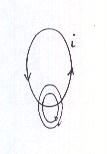
Соленоид – это катушка без сердечника. Магнитные силовые линии вокруг одного витка имеет вид:
В соленоиде магнитные силовые линии проходят следующим образом: (Рис.18)
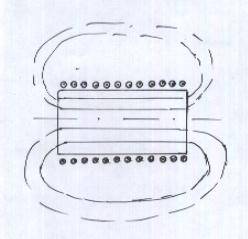
Внутри катушки – однородное магнитное поле. Вектор 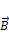 в любой точке параллелен оси соленоида.
в любой точке параллелен оси соленоида.
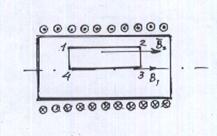
Выберем контур 1234. (рис.). Участок 34 лежит на оси соленоида. Запишем теорему о циркуляции вектора магнитной индукции:
Участок 4,1: 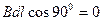
1,2: 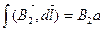
2,3: 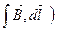 =0
=0
3,4 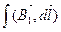 =
= 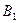
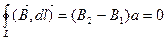
Так как контур токов не охватывает, 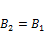 . Мы выбирали контур произвольно, поэтому в любой точке внутри соленоида магнитная индукция
. Мы выбирали контур произвольно, поэтому в любой точке внутри соленоида магнитная индукция 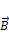 равна магнитной индукции на оси. Теперь выберем контур следующим образом: (Рис.20)
равна магнитной индукции на оси. Теперь выберем контур следующим образом: (Рис.20)
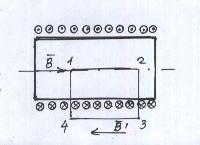
На участках 1,4 и 2,3:: 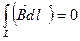
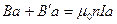
n – число витков на единицу длины соленоида. na – число витков на длине a.
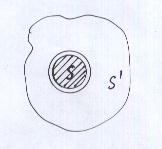
Докажем, что 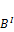 = 0. Возьмем плоскость перпендикулярную оси соленоида. Магнитные силовые линии всегда замкнуты. Магнитный поток
= 0. Возьмем плоскость перпендикулярную оси соленоида. Магнитные силовые линии всегда замкнуты. Магнитный поток 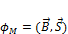 . В силу замкнутости магнитных силовых линий - поток внутри соленоида равен потоку вне соленоида.
. В силу замкнутости магнитных силовых линий - поток внутри соленоида равен потоку вне соленоида. 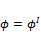 ,
, 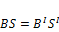 так как внешняя площадь
так как внешняя площадь 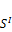 стремится к бесконечности,
стремится к бесконечности, 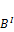 должно стремится к 0, то есть
должно стремится к 0, то есть 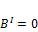 так как
так как 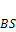 – конечно.
– конечно.
Таким образом, для соленоида: 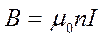
Величина nI имеет размерность: 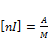 .
.
 2015-04-20
2015-04-20 1098
1098
