Решение. Для бесконечной последовательности испытаний в схеме Бернулли случайная величина Х, равная числу испытаний до первого успеха включительно

Для бесконечной последовательности испытаний в схеме Бернулли случайная величина Х, равная числу испытаний до первого успеха включительно, имеет геометрическое распределение:

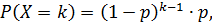
где р - вероятность успеха, равная 0,3.

Пусть случайная величина Х принимает значения 0,1,2,3…, к,…;

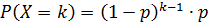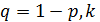, - число испытаний до первого успеха,

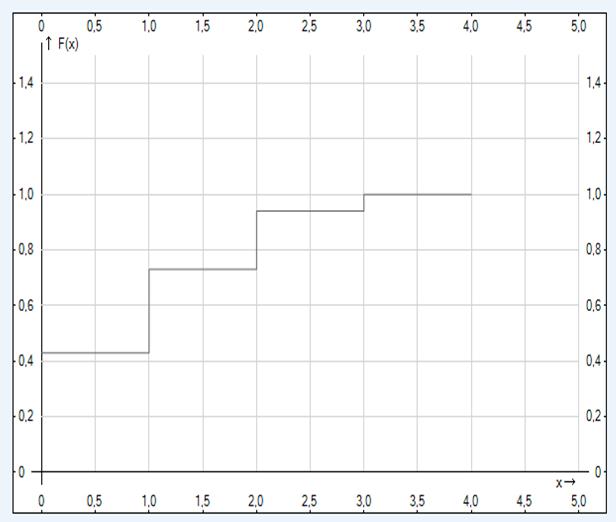
следовательно ряд распределения расставляется в виде:

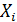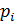	0,43	0,3	0,21	0,15

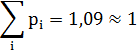
Используя формулу:

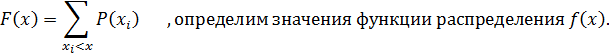
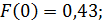
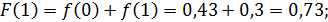
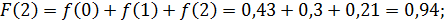
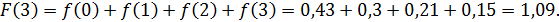
Математическое ожидание находим по формуле:

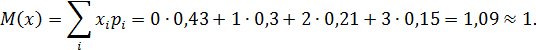
Ответ: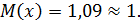

Задача 7.

Для случайной величины Х, распределенной по нормальному закону с параметрами 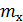=12 и σ = 3,1 определить вероятность попадания в интервал [9;14].