Тема 4 Дифференциальное уравнение равновесия жидкости

Выберем внутри покоящейся жидкости параллелепипед с рёбрами, параллельными координатным осям 0x, 0y, 0z и равными соответственно dx, dy и dz (рис. 7).

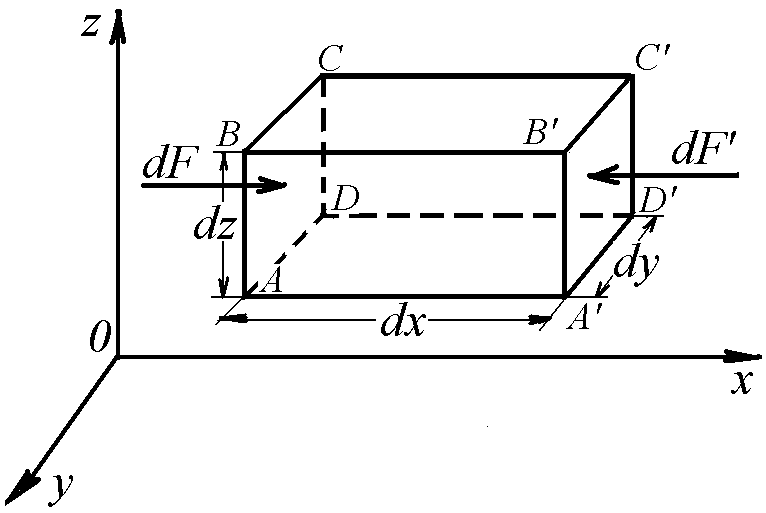
Рисунок 7 – К выводу дифференциального уравнения равновесия текучего тела

Составим уравнения равновесия этого параллелепипеда в виде уравнений проекций сил на координатные оси:

å F_x = 0; å F_y = 0; å F_z = 0

Проектируя силы на ось 0x имеем:

å F_x = dF – dF¢ + dG × cosa = 0, (4.1)

где dG – равнодействующая массовая (объёмная при r = const) сила;

a, b, g – углы, образованные равнодействующей массовой силой dG с координатными осями 0x, 0y и 0z соответственно;

dF и dF¢ – поверхностные силы, действующие на грани ABCD и A¢B¢C¢D¢.

Поверхностные силы dF и dF¢ равны:

dF = р × dy × dz; (4.2)

dF¢ = р¢ × dy × dz,

где р и р¢ – средние гидростатические давления на площадки ABCD и A¢B¢C¢D¢ соответственно.

Гидростатическое давление является функцией координат и при переходе от грани ABCD к грани A¢B¢C¢D¢ изменяется только координата x. Следовательно, можем записать:

р¢ = р + 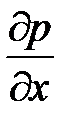× dx,

и сила dF¢ равна

dF¢ = (р + 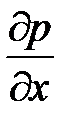× dx) × dy × dz. (4.3)

Проекция массовой силы равна:

dG × cosa = dm × j × cosa = r × d V × j × cosa = r × dx × dy × dz × j × cosa,

где j – ускорение массовой силы.

Обозначим проекции ускорения внешней массовой силы на координатные оси 0x, 0y и 0z:

X = j × cosa;

Y = j × cosb;

Z = j × cosg.

Проекция массовой силы равна:

dG × cosa = r × dx × dy × dz × X. (4.4)

Подставляя в уравнение (4.1) уравнения (4.2), (4.3) и (4.4), запишем:

р × dy × dz – (р + 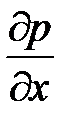× dx) × dy × dz + r × X × dx × dy × dz = 0.

Получаем уравнение проекций сил на ось 0x в виде:

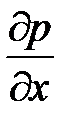– + r × X = 0.

Аналогично можно получить и уравнения проекций сил на оси 0y и 0z. Система уравнений равновесия жидкости (уравнения гидростатики Эйлера) запишется в виде:

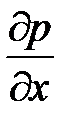– + r × X = 0;

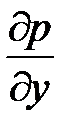– + r × Y = 0; (4.5)

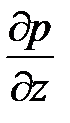– + r × Z = 0.

Таким образом, для равновесия массы жидкости необходимо, чтобы сумма всех внешних поверхностных и массовых сил, или их проекций на координатные оси равнялась нулю.

Умножив каждое из уравнений (4.5) соответственно на dx, dy и dz и сложив, получим:

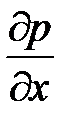× dx + 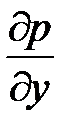× dy + 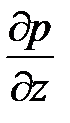× dz = r × X × dx + r × Y × dy + r × Z × dz.

Так как давление р зависит только от трёх независимых переменных координат x, y, z, левая часть последнего уравнения представляет собой полный дифференциал функции р = f (x, y, z):

dp = 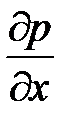× dx + 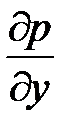× dy + 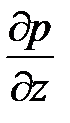× dz.

Тогда

dp = r × (X × dx + Y × dy + Z × dz). (4.6)