Проанализируем набор задач с характеристиками, представленными в Таблице 7.
Таблица 7: набор задач с коэффициентом использования равным 1
| Задача i | Время выполнения Ci | Период Ti | Отношение Ci/Ti | Загрузка (1.. N) | Граница |
| 0.25 | 0.25 | 1.000 | |||
| 0.40 | 0.65 | 0.828 | |||
| 0.35 | 1.00 | 0.779 |
.
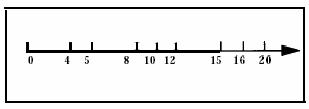
Рисунок 2: Точки диспетчеризации для трех задач, обсуждаемых в Примере 6.
l Шаг 1. Применяя Шаг 1, мы видим, что первые две задачи - диспетчируемы согласно ЧМА Теореме 1, но третья задача – нет. (Любопытно, что коэффициент совокупного использования равен 1. Это случается, особенно когда периоды задач гармонично связаны.) Поэтому, мы должны применить Теорему 2. Проделаем это с остальной частью эмпирического правила, данного выше.
l Шаг 2a. Определим все точки диспетчеризации со времени 0 до 20 (конец периода задачи самой низкой частоты). Точки диспетчеризации
для Задачи 1: 0, 4, 8, 12, 16, 20
для Задачи 2: 0, 5, 10, 15, 20
для Задачи 3: 0, 20
На оси времени, эти точки диспетчеризации появляются в порядке, представленном на Рисунке 2.
l Шаг 2b. Создайте неравенства для всех точек диспетчеризации. Неравенства:
C1 + C2, + C3 ≤ T 1
2 C1 + C2, + C3 ≤ T 2
2 C1 + 2 C2, + C3 ≤2 T 1
3 C1 + 2 C2, + C3 ≤2 T 2
3 C1 + 3 C2, + C3 ≤3 T 1
4 C1 + 3 C2, + C3 ≤3 T 2
4 C1 + 4 C2, + C3 ≤4 T 1
5 C1 + 4 C2, + C3 ≤ T 3
l Шаг 2c. Замените фактическими значениями все переменные, проверьте выполняется ли хотя бы одно из неравенств. Замены показаны ниже.
1+2+7>4
2*1+2+7>5
2*1 + 2*2+7>2*4
3*1 + 2*2+7>2*5
3*1 + 3*2+7>3*4
4*1 + 3*2+7>3*5
4*1 + 4*2+7>4*4
5*1 + 4*2+7=20
l Заключение. Набор задач из Таблицы 7 - диспетчеризуем, согласно Теореме 2, потому что одно из неравенств для третьей задачи выполняется.
В Примере 7, эмпирическое правило применено к набору задач, описанных в Таблице 6 из Примера 5.
 2015-04-30
2015-04-30 296
296








