Чтобы проиллюстрировать применение Теоремы 2, давайте проанализируем диспетчируемость задач, представленных в Таблице 6. Ясно, что эти три задачи - не диспетчеризируемы согласно ЧМА Теореме 1, потому что коэффициент совокупного использования центрального процессора для этих трех задач больше чем верхний предел (0.889> 0.779).
Чтобы проверить диспетчируемость этих трех задач из Таблицы 6, мы должны использовать уравнение Теоремы 2, только для i = 3, потому что первые две задачи диспетчеризируемы согласно Теореме 1. Таким образом, один из четырех индексов в этом уравнении фиксирован (i = 3). При расчете соответствующих сумм, другой индекс, j, изменяется от 1 до j = 3. Зная значения i и j, мы должны сосредоточиться на двух других индексах, k и l. Индекс k должен измениться от 1 до i = 3, и для каждого k, индекс, l должен изменить от 1 до 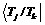 . Таким образом, значения всех четырех индексов задаются следующим образом:
. Таким образом, значения всех четырех индексов задаются следующим образом:
i =3
j =1…. 3
k= 1. .. 3
/=1... 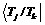
Дальнейшие вычисления просты, хотя очень громоздки.
k =1: 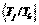 =
= 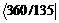 = 2; thus, l = 1, …, 2
= 2; thus, l = 1, …, 2
k =2: 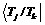 =
= 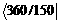 = 2; thus, l = 1, …, 2
= 2; thus, l = 1, …, 2
k =3: 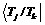 =
= 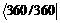 = 1;thus, l = 1.
= 1;thus, l = 1.
После некоторых вычислений мы получили следующие неравенства:
| l =1 | l =2 | |
| k =1 | >1 | ≤1 |
| k =2 | >1 | >1 |
| k =3 | >1 |
Из вышеупомянутого ясно, что, для k = 1 и / = 2, условие Теоремы 2 выполняется. Таким образом, набор трех задач из Таблицы 6 диспетчеризуем на основании алгоритма ЧМД.
К сожалению, условие Теоремы 2 сложно для понимания и громоздко для применения. Поэтому, мы предлагаем другую интерпретацию Теоремы 2, которая проще для понимания [5]. Суть теоремы заключается в том, что для определения диспетчируемости, достаточно и необходимо проверить, может ли каждая задача завершить свое выполнение перед первым критическим сроком. Технически, чтобы осуществить это, необходимо проверить множество неравенств для всех возможных точек диспетчеризации для каждой вовлеченной задачи, где точки диспетчеризации – это все моменты времени, в которые период любой задачи заканчивается. Эта проверка должна быть сделана для всех точек диспетчеризации, которые относятся к первому периоду каждой задачи, потому что гарантируется, что, если задача выполняется в ее первый критический срок, она будет всегда выполняться во все другие критические сроки.
Следующее эмпирическое правило может использоваться для упрощения проверки на диспетчируемость с помощью ЧМА
Шаг 1. Примените Теорему 1 и остановитесь, если все индивидуальные условия выполнены. В противном случае примените Теорему 2 для всех сомнительных случаев, как рекомендовано в следующих шагах (Шаги 2a - 2с).
Шаг 2a. Определите все точки диспетчеризации отмечая на оси времени все последовательные периоды для всех рассматриваемых задач, со времени 0 до конца первого периода самых низкочастотных задач.
Шаг 2b. Для всех точек диспетчеризации, отмеченных на шаге 2а, создается неравенство, которое имеет слева сумму всех возможных времен выполнения всех задач, которые могут быть активизированы (возможно, множественные времена) перед этой точкой диспетчеризации, а справа только значение времени, соответствующее этой точке диспетчеризации.
Шаг 2c. Проверьте, являются ли значения слева меньшими или равными соответствующим им значениям справа. Если хотя бы одно из этих неравенств выполняется, то набор задач диспетчируется согласно второй теореме ЧМА. В противном случае набор задач не диспетчируем согласно ЧМА
Пример 6 иллюстрирует вышеупомянутое эмпирическое правило.
 2015-04-30
2015-04-30 236
236








