1.Интегралы вида 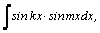
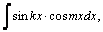
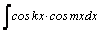 вычисляются преобразованием произведения тригонометрических функций в сумму по формулам:
вычисляются преобразованием произведения тригонометрических функций в сумму по формулам:
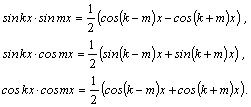
Например, 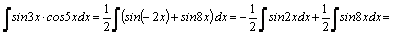
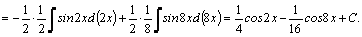
2.Интегралы вида 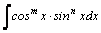 , где m или n– нечетное положительное число, вычисляются подведением под знак дифференциала.
, где m или n– нечетное положительное число, вычисляются подведением под знак дифференциала.
Например,

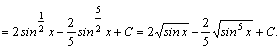
3.Интегралы вида 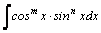 , где m и n–четные положительные числа, вычисляются с помощью формул понижения степени:
, где m и n–четные положительные числа, вычисляются с помощью формул понижения степени:
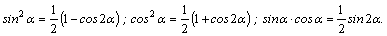
Например,
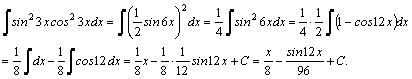
4.Интегралы 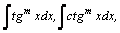 где
где 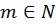 , вычисляются заменой переменной:
, вычисляются заменой переменной: 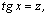
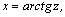
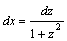 или
или 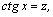
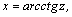
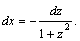
Например,
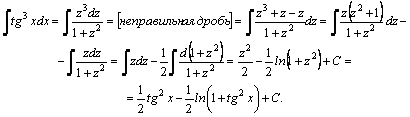
 2015-05-05
2015-05-05 332
332







