1. Пользуясь определением предела функции по Гейне, сформулировать определение того, что функция 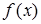 не имеет предела в точке a.
не имеет предела в точке a.
Решение. Запишем определение предела функции в точке по Гейне:
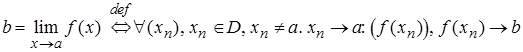 .
.
Тогда, построив отрицание этого высказывания по известным правилам, получаем:
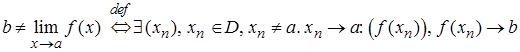 .
.
Число b не является пределом функции 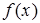 в точке a, если существует последовательность
в точке a, если существует последовательность 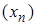 ,
, 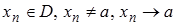 , такая, что соответствующая последовательность значений функции
, такая, что соответствующая последовательность значений функции 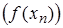 не сходится к числу b. Если это предложение верно
не сходится к числу b. Если это предложение верно 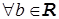 , т.е. никакое число b не является пределом функции
, т.е. никакое число b не является пределом функции 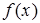 в точке a, то эта функция вообще не имеет предела в точке a.
в точке a, то эта функция вообще не имеет предела в точке a.
Таким образом, чтобы доказать, что функция в точке не имеет предела, достаточно показать существование двух последовательностей 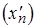 ,
, 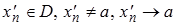 , и
, и 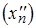 ,
, 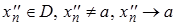 , для которых соответствующие последовательности значений функции
, для которых соответствующие последовательности значений функции 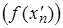 и
и 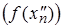 сходятся к разным числам
сходятся к разным числам 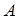 и
и 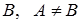 . В этом случае (см. выше) ни число
. В этом случае (см. выше) ни число 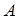 , ни число
, ни число 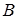 , ни какое-либо другое число не могут быть пределом функции
, ни какое-либо другое число не могут быть пределом функции 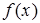 в точке a, т.е. функции
в точке a, т.е. функции 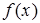 не имеет предела в точке a.
не имеет предела в точке a.
Другой способ доказать отсутствие предела заключается в том, чтобы привести пример хотя бы одной последовательности 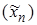 , для которой последовательность значений функции
, для которой последовательность значений функции 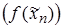 вообще не имеет предела.
вообще не имеет предела.
2. Используя результат предыдущего примера, показать, что функция 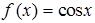 при
при 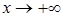 не имеет предела.
не имеет предела.
Решение. I способ. Выберем две последовательности точек 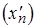 ,
, 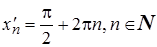 , и
, и 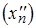 ,
, 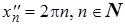 . Обе эти последовательности стремятся к
. Обе эти последовательности стремятся к 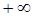 . Им соответствуют последовательности значений функций:
. Им соответствуют последовательности значений функций:
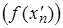 ,
, 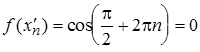 ,
,
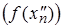 ,
, 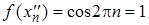 .
.
Последовательности значений функции 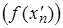 и
и 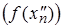 - стационарные, сходятся к числам
- стационарные, сходятся к числам 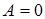 и
и 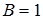 соответственно. Так как
соответственно. Так как 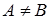 , то (см. пример 1) функция
, то (см. пример 1) функция 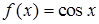 не имеет предела при
не имеет предела при 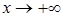 .
.
II способ. Выберем последовательность 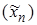 ,
, 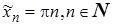 ,
, 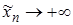 . Ей соответствует последовательность значений функции
. Ей соответствует последовательность значений функции 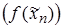 ,
, 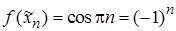 , которая вообще не имеет предела. Следовательно (см. пример 1), функция
, которая вообще не имеет предела. Следовательно (см. пример 1), функция 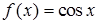 не имеет предела при
не имеет предела при 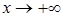 .
.
3. Доказать по определению Коши, что 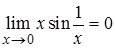 .
.
Решение. Областью определения функции 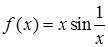 является множество
является множество 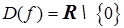 . Точка
. Точка 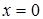 не принадлежит области определения функции
не принадлежит области определения функции 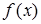 , но является предельной точкой множества
, но является предельной точкой множества 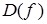 . Это говорит о том, что имеет смысл рассматривать поведение функции
. Это говорит о том, что имеет смысл рассматривать поведение функции 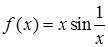 при приближении к точке
при приближении к точке 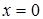 , т.е. имеет смысл выражение
, т.е. имеет смысл выражение 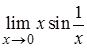 . Докажем, что этот предел равен нулю, т.е. согласно определению предела функции по Коши необходимо показать справедливость утверждения:
. Докажем, что этот предел равен нулю, т.е. согласно определению предела функции по Коши необходимо показать справедливость утверждения:
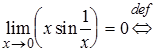
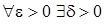

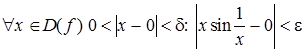 ,
,
т.е. 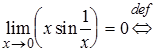
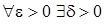

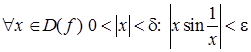 .
.
Выберем произвольное 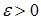 . Выясним, при каких
. Выясним, при каких 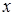 верно неравенство
верно неравенство 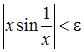 . Если мы получим, например, что неравенство
. Если мы получим, например, что неравенство 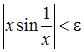 верно при
верно при 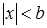 (число
(число 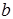 , вообще говоря, может зависеть от
, вообще говоря, может зависеть от 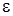 ), то это число
), то это число 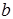 и можно выбрать в качестве
и можно выбрать в качестве 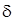 .
.
Используя свойства модуля и ограниченность функции 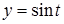
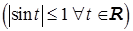 , получаем:
, получаем: 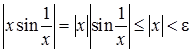 . Т.е. если для некоторого
. Т.е. если для некоторого 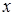 выполняется неравенство
выполняется неравенство 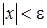 , то в силу транзитивности для этого
, то в силу транзитивности для этого 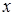 обязательно выполняется неравенство
обязательно выполняется неравенство 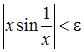 . Значит, в качестве
. Значит, в качестве 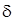 можно выбрать само число
можно выбрать само число 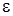 (или любое число, меньшее
(или любое число, меньшее 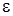 ).
).
Таким образом, мы показали, что
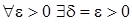

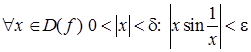 ,
,
а это по определению Коши и означает, что 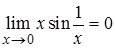 .
.
4. Доказать по определению Коши, что 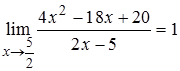 .
.
Решение. Согласно определению предела функции по Коши необходимо показать справедливость утверждения:
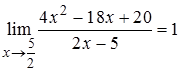
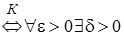
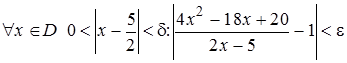 .
.
Выберем произвольное 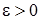 . Задача состоит в том, чтобы для этого
. Задача состоит в том, чтобы для этого 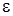 найти такое
найти такое 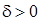 , при котором из неравенства
, при котором из неравенства 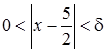 следовало бы неравенство
следовало бы неравенство 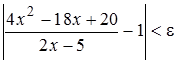 .
.
Выясним, когда верно последнее неравенство 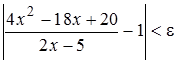 . При этом нас будет интересовать не при каких
. При этом нас будет интересовать не при каких 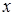 верно это неравенство, а при каких
верно это неравенство, а при каких 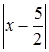 . Если мы получим, например, что неравенство
. Если мы получим, например, что неравенство 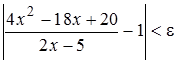 верно при
верно при 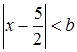 (
(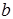 , вообще говоря, может зависеть от
, вообще говоря, может зависеть от 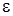 ), то это число
), то это число 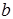 и можно выбрать в качестве
и можно выбрать в качестве 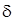 .
.
Проводим следующие преобразования неравенства: приводим выражение под знаком модуля к общему знаменателю, приводим подобные слагаемые, раскладываем на множители числитель и сокращаем на общий множитель дробь:
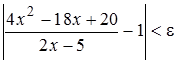 ,
, 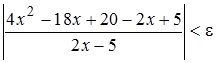 ,
, 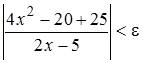 ,
,
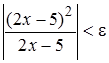 ,
, 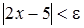 ,
, 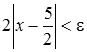 ,
, 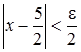 .
.
Следовательно, в качестве 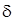 можно взять
можно взять 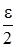 .
.
Таким образом, мы показали, что:
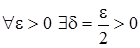
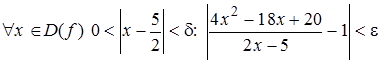 ,
,
а это и означает по определению Коши, что 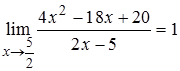 .
.
5. Сформулировать определения по Гейне и по Коши, соответствующие следующим символическим обозначениям: а) 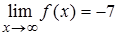 ; б)
; б) 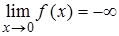 .
.
Решение. а) Запишем определение по Гейне, учитывая, что 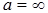 ,
, 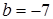 :
: 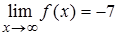
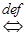
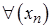 ,
, 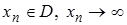 :
: 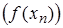 ,
, 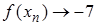 .
.
Определение по Коши получим с помощью общего определения предела:
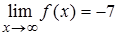
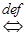
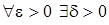
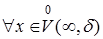 :
: 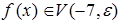 .
.
Учитывая, что 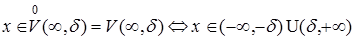 , т.е.
, т.е. 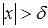 , и
, и 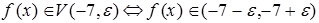 , т.е.
, т.е. 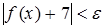 , получаем определение предела функции по Коши:
, получаем определение предела функции по Коши:
|

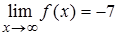
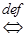
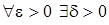
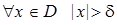 :
: 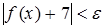 .
.
|
|
|

 Геометрический смысл: при
Геометрический смысл: при 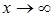 график функции
график функции 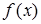 приближается к прямой
приближается к прямой 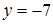 . На рисунке изображен график функции, для которой
. На рисунке изображен график функции, для которой 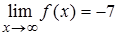 .
. б) Запишем определение по Гейне, учитывая, что 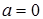 ,
, 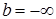 :
:
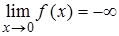
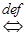
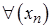 ,
, 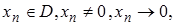 :
: 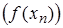 ,
, 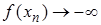 .
.
Определение Коши построим, исходя из общего определения предела:
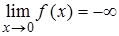
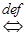
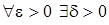
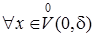 :
: 
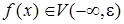 .
.
Учитывая, что 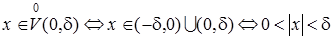
и 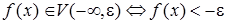 , получаем:
, получаем:
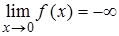
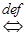
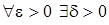
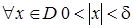 :
: 
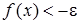 .
.
6. Доказать, что 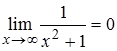 .
.
Решение. С помощью определения 3 построим утверждение, которое нам необходимо доказать:
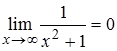
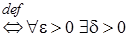
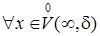 :
: 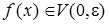 .
.
Записав окрестности в виде неравенств, получаем:
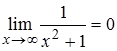
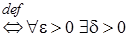
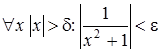 .
.
Докажем последнее утверждение. Выберем произвольное 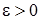 . Необходимо для этого
. Необходимо для этого 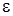 найти такое
найти такое 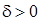 , при котором из неравенства
, при котором из неравенства 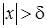 следует неравенство
следует неравенство 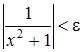 .
.
Решим последнее неравенство 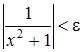 (при этом решение ищем в виде
(при этом решение ищем в виде 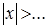 ).
).
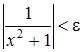 ,
, 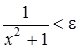 ,
, 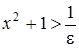 ,
, 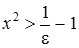
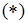 ,
, 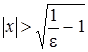 .
.
Если 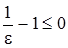 (т.е. если
(т.е. если 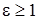 ), то неравенство
), то неравенство 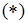 , а, значит, и
, а, значит, и 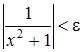 , верно
, верно 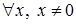 . Тогда в качестве
. Тогда в качестве 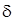 можно брать любое положительное число (например,
можно брать любое положительное число (например, 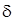 =1).
=1).
Если 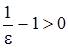 , то в качестве
, то в качестве 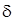 можно взять число
можно взять число 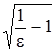 (и любое большее).
(и любое большее).
|
 Следовательно, мы показали, что для любого
Следовательно, мы показали, что для любого 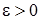 существует
существует 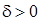 (
(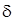 -любое
-любое 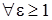 и
и 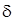 =
= 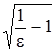
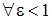 ) такое, что
) такое, что 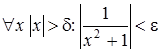 . Тогда по определению
. Тогда по определению 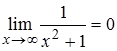 .
.
|
|
|
 Геометрический смысл предела
Геометрический смысл предела 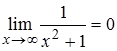 : при больших по модулю значениях аргумента график функции
: при больших по модулю значениях аргумента график функции 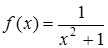 приближается к прямой
приближается к прямой 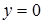 , т.е. к оси абсцисс.
, т.е. к оси абсцисс. 7. Записать утверждение в предельной форме, т.е. в виде 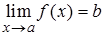 :
:
а) 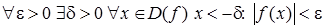 ;
;
б) 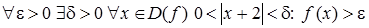 .
.
Решение. а) В этом примере необходимо решить задачу, обратную задаче примера 5. Сначала перепишем данное высказывание на "языке окрестностей":
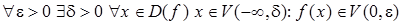 .
.
Затем, сравнивая получившееся высказывание с определением 3, получаем, что 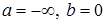 . Следовательно, данное утверждение в предельной форме можно записать так:
. Следовательно, данное утверждение в предельной форме можно записать так: 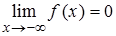 .
.
б) Данное утверждение 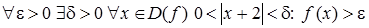 перепишем на "языке окрестностей":
перепишем на "языке окрестностей":
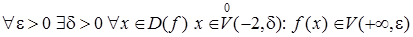 .
.
Тогда 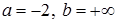 . Следовательно,
. Следовательно,
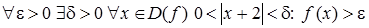
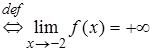 .
.
 2015-05-05
2015-05-05 17495
17495