2015-05-05
651
Определим количество критериев подобия, необходимых для описания нестационарного течения вязкой несжимаемой жидкости, воспользовавшись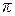 
-теоремой.
Независимыми переменными, определяющими рассматриваемый процесс, являются скорость жидкости W; давление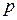 
(или перепад давлений 
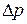) в системе; характерный линейный размер системы L; время 
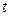; теплофизические свойства среды, такие как плотность ρ и динамический коэффициент вязкости μ.
Размерности и формулы размерностей для всех определяющих величин в системе СИ приведены в таблице 7.1, где знаком "√" обозначены величины, которые будем считать величинами с независимой размерностью.
Таблица 7.1 - Список и формулы размерности величин, определяющих процесс нестационарного течения несжимаемой среды
| № | Определяющие физические величины | Обозна- чение | Наименование размерности | Формула размерности |
| Скорость | W | м / с |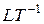 
| |
| Давление |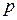
| 
| 
| |
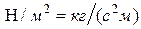
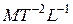
| Характерный линейный размер cистемы |  √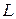
| м | L | |
| Время |  √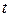
| с |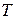 
| |
| Плотность среды |  √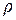
| кг / м3 |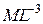 
| |
| Динамический коэффициент вязкости среды | μ |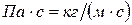 
| 
|
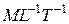
Итак, в рассматриваемой задаче имеется шесть определяющих величин, из которых три имеют независимую размерность (например, 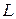, 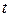и 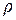), т.е. 
, 
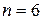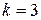. Следовательно, в соответствии с p - теоремой, для описания рассматриваемого явления число независимых критериев подобия должно быть равно трем (
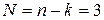), а, значит, в данном случае вместо поиска функциональной зависимости между шестью величинами в размерном уравнении
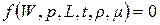
необходимо найти связь между тремя безразмерными критериями подобия
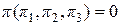. (7.13)
Таким образом, как уже отмечалось, хотя теория размерностей не позволяет установить функциональную зависимость между критериями подобия, однако она дает возможность уменьшить число определяющих переменных и обеспечивает основу для планирования и проведения экспериментов.
