Топология – фигураларды үзу немесе желімдеуден басқа кез келген диформация жасағанда олардың өзгермей қалатын қасиеттерін оқытатын математиканың бөлімі. Дәлірек айтсақ, өзара бірмәнді және үздіксіз бейнелеулерде фигуралардың өзгермей қалатын қасиеттерін зерттейтін математиканың бөлімі.
Мысалы: Шеңбер, эллипс, квадрат контурларының топологиялық қасиеттері бірдей. Себебі, олардың біреуі екіншісін, жоғарыда айтқандай, диформация арқылы алынады. Ал дөңгелек, сақина фигураларының топологиялық қасиеттері әртурлі. Себебі, дөңгелекте 1 контур, ал сақинада 2 контур.
1. Метрикалық кеңістіктер, мысалдары.
Е – құр емес жиын болсын.
Анықтама. Е жиынында 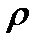 метрикасы берілген деп аталады, егер
метрикасы берілген деп аталады, егер 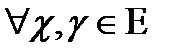 элементтер қосына төмендегі шарттарды қанағаттандыратын
элементтер қосына төмендегі шарттарды қанағаттандыратын 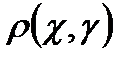 нақты саны сәйкес қойылған болса
нақты саны сәйкес қойылған болса
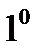
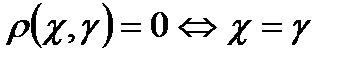
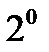
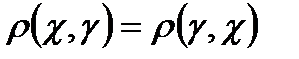
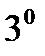
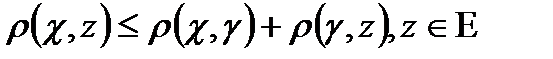
Немесе, метрика анықтамасын басқаша беруге болады.
Анықтама. Е жиынындағы метрика деп 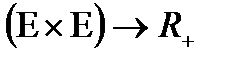 бейнелеуін айтады. Мұндағы,
бейнелеуін айтады. Мұндағы, 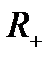 - теріс емес нақты сандар жиыны.
- теріс емес нақты сандар жиыны.
Метрика берілген Е жиынын метрикалық кеңістік деп атайды. Белгіленуі 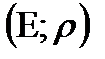 , ал оның элементтерін
, ал оның элементтерін 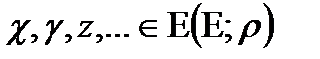 метрикалық кеңістігінің нүктелері деп аталады.
метрикалық кеңістігінің нүктелері деп аталады.
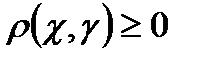 саны
саны 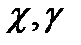 нуктелерінің арақашықтығы деп аталады.
нуктелерінің арақашықтығы деп аталады. 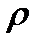 функциясының
функциясының 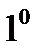 ,
, 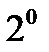 ,
, 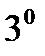 қасиеттерін метрикалық кеңістіктің аксиомалары деп атайды.
қасиеттерін метрикалық кеңістіктің аксиомалары деп атайды.
Мысалдар:
1) 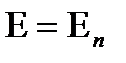 , мұнда
, мұнда 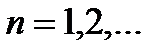 Евклидтік кеңістігінде
Евклидтік кеңістігінде 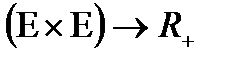 бейнелеуін
бейнелеуін 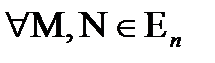
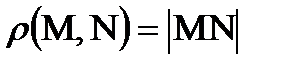 заңдылығы бойынша енгізейік, онда
заңдылығы бойынша енгізейік, онда 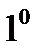 ,
, 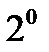 ,
, 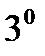 аксиомалары орындалатынын байқау жеңіл. Олай болса,
аксиомалары орындалатынын байқау жеңіл. Олай болса, 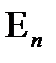 - метрикалық кеңістік.
- метрикалық кеңістік.
2) 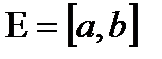 сан кесіндісі болсын, яғни
сан кесіндісі болсын, яғни 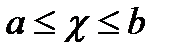 қанағаттандыратын нақты сандар жиыны Метриканың
қанағаттандыратын нақты сандар жиыны Метриканың 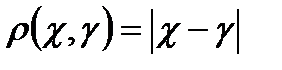 заңдылығы бойынша енгізейік. Онда
заңдылығы бойынша енгізейік. Онда 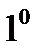 ,
, 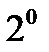 аксиомалары орындалатынын байқау жеңіл.
аксиомалары орындалатынын байқау жеңіл.
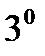 аксиоманың орындалатынын дәлелдейік. Айталық,
аксиоманың орындалатынын дәлелдейік. Айталық, 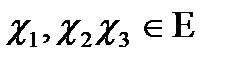 .
.
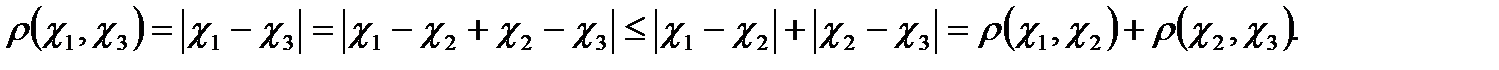
яғни 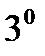 аксиома орындалады. Олай болса, Е жиыны метрикалық кеңістік.
аксиома орындалады. Олай болса, Е жиыны метрикалық кеңістік.
3) 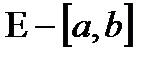 сегментінде үздіксіз барлық сан функцияның жиыны болсын. Егер метриканы
сегментінде үздіксіз барлық сан функцияның жиыны болсын. Егер метриканы 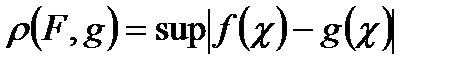 заңдылығы бойынша енгізейік, мұнда
заңдылығы бойынша енгізейік, мұнда 
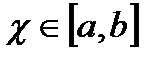 .
.
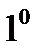 ,
, 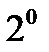 аксиомалары орындалатыны айқын,
аксиомалары орындалатыны айқын, 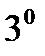 аксиомасының орындалатынын көрсетейі
аксиомасының орындалатынын көрсетейі
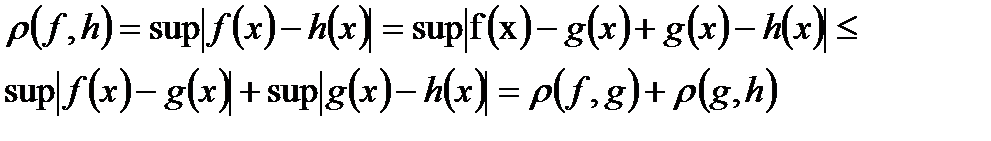
Сонымен, 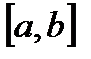 сегментінде үздіксіз сан функцияның жиыны метрикалық кеңістік болады. Оны
сегментінде үздіксіз сан функцияның жиыны метрикалық кеңістік болады. Оны 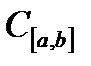 түрінде белгілейді.
түрінде белгілейді.
2. Ашық жиындар.
Айталық, 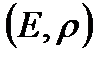 метрикалық кеңістік берілсін.
метрикалық кеңістік берілсін.
Анықтама. Центрі 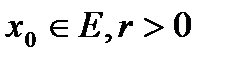 болатын ашық шар деп
болатын ашық шар деп 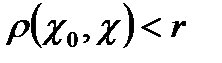 шардың қанағаттандыратын барлық
шардың қанағаттандыратын барлық 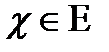 жиынын айтады.
жиынын айтады. 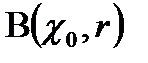 түрінде белгілейді. Ал
түрінде белгілейді. Ал 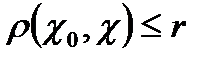 шартын қанағаттандыратын
шартын қанағаттандыратын 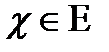 -ге нүктенің жиынын жабық шар деп атайды.
-ге нүктенің жиынын жабық шар деп атайды. 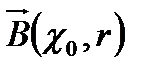 деп белгіленеді,
деп белгіленеді, 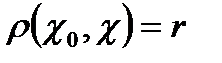 шартын қанағаттандыратын
шартын қанағаттандыратын 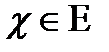 нүктесінің жиынын сфера деп атайды.
нүктесінің жиынын сфера деп атайды. 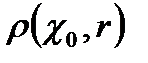 түрінде белгіленеді.
түрінде белгіленеді.
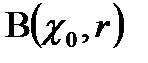 ашық шарын
ашық шарын 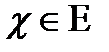 нүктесінің маңайы деп атайды.
нүктесінің маңайы деп атайды.
Анықтама. А жиыны 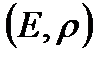 метрикалық кеңістігінің құр емес ішкі бөлігі болсын.
метрикалық кеңістігінің құр емес ішкі бөлігі болсын. 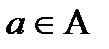 нүктесі А жиынының ішкі нүктесі деп аталады. Егер оның А жиынына түгелімен енетін маңайы бар болса.
нүктесі А жиынының ішкі нүктесі деп аталады. Егер оның А жиынына түгелімен енетін маңайы бар болса.
Анықтама. Әрбір нүктесі ішкі нүкте болатын жиын ашық жиын деп аталады.
Мысал: Сан интервалы, ашық дөңгелек, ашық жиындар.
Анықтама. 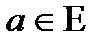 нүктесі А жиынының сыртқы нүктесі деп аталады, егер оның А жиынының нүктесін қамтитын Е маңайы бар болса.
нүктесі А жиынының сыртқы нүктесі деп аталады, егер оның А жиынының нүктесін қамтитын Е маңайы бар болса.
Анықтама. 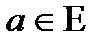 нүктесі А жиынының шекаралық нүктесі деп аталады, егер оның әрбір Е маңайының А және
нүктесі А жиынының шекаралық нүктесі деп аталады, егер оның әрбір Е маңайының А және 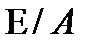 жиынының әрқайсысымен қималары құр емес жиын болса.
жиынының әрқайсысымен қималары құр емес жиын болса.
Анықтама. Барлық шекаралық нүктелер жиыны А жиынының шекарасы деп аталады.
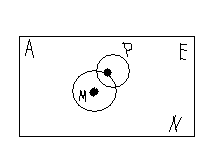
М- ішкі нүкте, P- шекаралық нүкте, N- сыртқы нүкте
Анықтама. 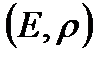 метрикалық кеңістігінің А жиыны шектелген деп аталады, егер оны тұтастай қамтитын шар бар болса.
метрикалық кеңістігінің А жиыны шектелген деп аталады, егер оны тұтастай қамтитын шар бар болса.
Мысал: эллипс, көпбұрыш, дөңгелек, шектелген жиындар.Ал парабола, гипербола,синусоида шектелмеген жиындар.
Теорема. 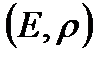 метрикалық кеңістігінің барлық ашық жиынының жиынын
метрикалық кеңістігінің барлық ашық жиынының жиынын 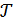 делік.
делік.
Метрикалық кеңістіктің 1)ашық жиынның кез келген тобының бірігуі ашық жиын болады; 2) ашық жиынның саны шекті кез келген тобының қимасы ашық жиын болады.
Дәлелдеуі: 1) 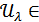
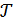 делік, яғни
делік, яғни 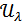 -
- 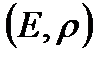 метрикалық кеңістігінің ашық жиын. Мұнда
метрикалық кеңістігінің ашық жиын. Мұнда 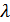 кейбір
кейбір 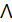 жиынында өзгереді. (
жиынында өзгереді. (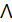 - шексізжиын болуы мүмкін). Барлық
- шексізжиын болуы мүмкін). Барлық 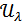 жиындарының бірігуін қарастырайық және оны
жиындарының бірігуін қарастырайық және оны 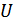 әрпімен белгілейік.
әрпімен белгілейік.
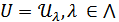 (1)
(1)
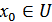 кез келген нүктесін алайық. (1) теңдікті ескерсек
кез келген нүктесін алайық. (1) теңдікті ескерсек 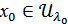 болатын ең болмағанда бір
болатын ең болмағанда бір 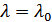 индексі табылады.
индексі табылады. 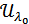 – ашық жиын болғандықтан оның
– ашық жиын болғандықтан оның 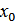 нүктесінің
нүктесінің 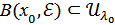 болатындай
болатындай 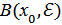 маңайы табылады.
маңайы табылады. 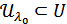 болғандықтан
болғандықтан 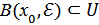 . Сонымен кез келген
. Сонымен кез келген 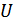 жиынының кез келген
жиынының кез келген 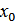 нүктесінің тұтастай
нүктесінің тұтастай 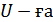 енетін
енетін 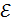 маңайы табылады. Олай болса
маңайы табылады. Олай болса 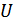 – ашық жиын.
– ашық жиын.
Теореманың 2) бөлігін 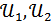 ашық жиын үшін дәлелдеу жеткілікті. Егер
ашық жиын үшін дәлелдеу жеткілікті. Егер
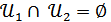 болса, онда 2) ұйғарым дәлелденді, себебі
болса, онда 2) ұйғарым дәлелденді, себебі 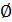 жиын ашық жиын.
жиын ашық жиын.
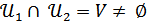 жағдайын қарастырайық.
жағдайын қарастырайық. 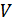 жиынындағы
жиынындағы 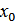 нүктесі үшін
нүктесі үшін 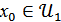 ,
, 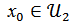 болады.
болады. 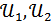 - ашық жиындар болғандықтан
- ашық жиындар болғандықтан 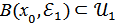 ,
,
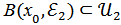 болатындай
болатындай 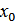 нүктесінің
нүктесінің 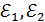 маңайлары табылады. Егер
маңайлары табылады. Егер 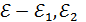 сандарын ең кішісі десек
сандарын ең кішісі десек 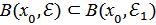 ,және
,және 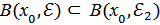 болады. Олай болса,
болады. Олай болса, 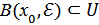 , яғни
, яғни 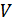 жиыны өзінің әрбір нүктесімен қатар, осы нүктенің
жиыны өзінің әрбір нүктесімен қатар, осы нүктенің 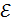 маңайын қамтиды. Олай болса,
маңайын қамтиды. Олай болса, 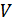 – ашық жиын. Теорема толық дәлелденді.
– ашық жиын. Теорема толық дәлелденді.
1. Топологиялық кеңістік ұғымы, мысалдары.
Айталық Х жиынында кейбір тәсілмен төмендегі қасиеттерге ие болатын ішкі жиындар жүйесі бөлінген болсын. Осы жүйені Р дейік (Р- барлық ішкі жиындар жиыны емес).
Анықтама. Егер Х жиынында төмендегі шарттарды қанағаттандыратын ішкі жиындар жүйесі алынған болса, онда Х жиынында топологиялық структура немесе топология анықталған делінеді.
I. 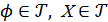
II. Г жүйесіндегі ішкі жиынның кез келген тобының бірігуі 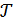 жүйесіне тиісті.
жүйесіне тиісті.
III. Г жүйесіндегі ішкі жиынның саны шекті тобының қимасы 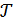 жүйесіне тиісті.
жүйесіне тиісті.
(Х,  қосын топологиялық кеңістік деп атайды.
қосын топологиялық кеңістік деп атайды.
I, II, III қасиеттер топологиялық кеңістігінің аксиомалары деп аталады.
Х жиынының элементтерін (Х,  топологиялық кеңістігінің нүктелері, ал
топологиялық кеңістігінің нүктелері, ал 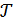 жүйесінің элементтерін осы топологиялық кеңістігінің (Х,
жүйесінің элементтерін осы топологиялық кеңістігінің (Х,  түрінде жазбай, кейде тек Х арқылы да белгілейді.
түрінде жазбай, кейде тек Х арқылы да белгілейді.
Мысал.
1. 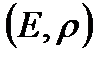 метрикалық кеңістігі берілсін. Жоғарыдағы теорема бойынша бұл метрикалық кеңістік топологиялық кеңістік болатынын көреміз және оның топологиясы ашық шарлар жиыны болады. Бұл кеңістіктің топологиясы
метрикалық кеңістігі берілсін. Жоғарыдағы теорема бойынша бұл метрикалық кеңістік топологиялық кеңістік болатынын көреміз және оның топологиясы ашық шарлар жиыны болады. Бұл кеңістіктің топологиясы 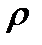 метрикасымен индуцирленген деп аталады.
метрикасымен индуцирленген деп аталады.
2. Х кейбір жиыны берілсін.
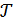 - Х жиынының барлық ішкі жиынының жиыны болсын. Онда I, II, III аксиомасы орындалатынын көреміз.Олай болса, (Х,
- Х жиынының барлық ішкі жиынының жиыны болсын. Онда I, II, III аксиомасы орындалатынын көреміз.Олай болса, (Х,  топологиялық кеңістік болады және мұндай топологияны дискретті топология деп атайды.
топологиялық кеңістік болады және мұндай топологияны дискретті топология деп атайды.
3. Егер (Х,  қосы тек екі жиыннан
қосы тек екі жиыннан 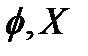 тұрса, мұндай топологиялық кеңістікті антидискретті топологиялық кеңістік деп атайды.
тұрса, мұндай топологиялық кеңістікті антидискретті топологиялық кеңістік деп атайды.
2, 3 мысалдар кез келген Х жиынын топологиялық кеңістікке айналдыруға болатын көрсетеді.
Анықтама. Айталық, (Х,  топологиялық кеңістігі берілсін.
топологиялық кеңістігі берілсін. 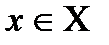 нүктесін қамтитын V ашық жиынды осы нүктенің маңайы деп атайды. Бұл анықтамадан
нүктесін қамтитын V ашық жиынды осы нүктенің маңайы деп атайды. Бұл анықтамадан 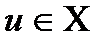 ішкі жиыны өзінің х нүктесінің маңайы болу үшін оның ашық жиын болуы қажетті және жеткілікті екені шығады, яғни
ішкі жиыны өзінің х нүктесінің маңайы болу үшін оның ашық жиын болуы қажетті және жеткілікті екені шығады, яғни 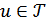 болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті.
2. Топологияның базасы.
Анықтама. (Х,  топологиялық кеңістігінің ішкі жиынының тобы В -
топологиялық кеңістігінің ішкі жиынының тобы В - 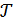 топологияның базасы деп аталады, егер
топологияның базасы деп аталады, егер 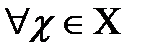 нүктесі және оның кез келген
нүктесі және оның кез келген 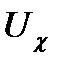 маңайы үшін
маңайы үшін 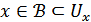 шарты орындалатындай
шарты орындалатындай 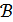 жиынының
жиынының 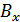 элементі табылса
элементі табылса
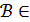 (Х,
(Х,  (топологиялық кеңістігінің базасы)
(топологиялық кеңістігінің базасы) 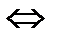 (
(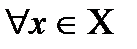
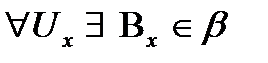
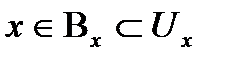 )
)
Мысал: Интервалдар жиыны R жиынында берілген топологиялық база болады.
Кез келген 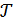 топологиясы үшін база табылады. Себебі Г тобының өзі база болады.
топологиясы үшін база табылады. Себебі Г тобының өзі база болады.
Анықтама. (Х,  топологиялық кеңістігі
топологиялық кеңістігі 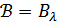 - осы топологиялық кеңістігінің ашық жиынының кейбір тобы болсын. Егер (Х,
- осы топологиялық кеңістігінің ашық жиынының кейбір тобы болсын. Егер (Х,  кеңістігінің кез келген ашық жиыны
кеңістігінің кез келген ашық жиыны 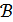 тобының кейбір жиынының бірігуі болса, онда
тобының кейбір жиынының бірігуі болса, онда 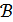 (Х,
(Х,  топологиялық кеңістігінің базасы деп аталады.
топологиялық кеңістігінің базасы деп аталады.
Базаның негізгі қасиеті:
Теорема. (Х,  топологиялық кеңістігінің ашық жиынының
топологиялық кеңістігінің ашық жиынының 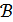 тобы
тобы 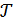 топологиясының базасы болу үшін
топологиясының базасы болу үшін 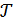 - ның әрбір элементі
- ның әрбір элементі 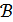 тобының кейбір элементінің бірігуі болуы қажетті және жеткілікті.
тобының кейбір элементінің бірігуі болуы қажетті және жеткілікті.
Дәлелдеуі:
1) Қажеттілік шарт. 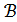 -
- 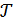 топологиясының базасы,
топологиясының базасы, 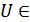
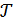 болсын. Базаны анықтамасы бойынша
болсын. Базаны анықтамасы бойынша 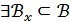 Х
Х 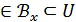
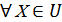 нүктелері үшін
нүктелері үшін 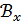 (ашық жиынының) элементтерінің жиынын қарастырсақ, мұндай
(ашық жиынының) элементтерінің жиынын қарастырсақ, мұндай 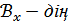 бірігуі
бірігуі 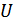 болатыны айқын.
болатыны айқын.
Кері ұйғарымды дәлелдеу жеңіл. Теорема толық дәлелденді.
Анықтама. (Х,  кеңістігі саналатын базаны кеңістік деп атайды, егер
кеңістігі саналатын базаны кеңістік деп атайды, егер 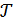 топологиясында Х жиынының ашық ішкі жиынының шекті немесе саналатын тобынан тұратын ең болмағанда бір база бар болса.
топологиясында Х жиынының ашық ішкі жиынының шекті немесе саналатын тобынан тұратын ең болмағанда бір база бар болса.
5. Жиынның тұйықтық шарты.
А - (Х,  топологиялық кеңістігінің құр емес жиыны болсын.
топологиялық кеңістігінің құр емес жиыны болсын.
А жиынының барлық ішкі нүктесінің жиыны оның іші деп аталады. 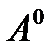 түрінде белгіленеді. А ашық жиын болу үшін ол өзінің ішімен беттесуі қажетті және жеткілікті.
түрінде белгіленеді. А ашық жиын болу үшін ол өзінің ішімен беттесуі қажетті және жеткілікті.
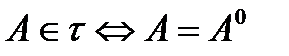
Анықтама. Х нүктесі А жиынының жанасу нүктесі деп аталады, егер оның кез келген маңайының А жиыны мен қимасы құр емес жиын болса.
Ан. А жиынының барлық жанасу нүктесінен тұратын жиын А жиынының тұйықталуы деп аталады. А түрінде белгіленеді.
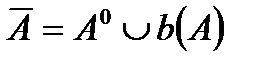 , мұн b(A) – А жиынның шекарасы.
, мұн b(A) – А жиынның шекарасы.
Мыс: А=(а,b) болса, онда 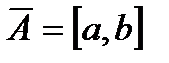 болады. Ашық дөңгелектің тұйыталуы жабық болады.
болады. Ашық дөңгелектің тұйыталуы жабық болады.
Ан. А жиыны (Х,  топологиялық кеңістігінде тұйық деп аталады, егер с А ашық жиын болса.
топологиялық кеңістігінде тұйық деп аталады, егер с А ашық жиын болса.
Мыс: 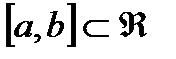 тұық жиыны
тұық жиыны 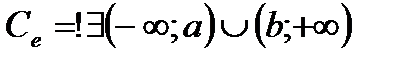 Жабық шар.
Жабық шар.
Теорема. (жиынның тұйық белгісі) 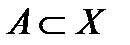 топологиялық кеңістікте тұйық жиын болу үшін оның өзінің тұйқталуы мен беттесуі қажетті және жеткілікті.
топологиялық кеңістікте тұйық жиын болу үшін оның өзінің тұйқталуы мен беттесуі қажетті және жеткілікті.
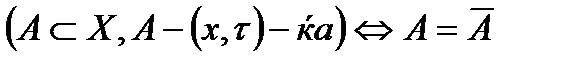
Дәлелдеуі: 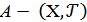 кеңістігінде тұйық жиын болсын, онда
кеңістігінде тұйық жиын болсын, онда 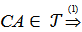
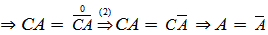 дәлелденді.
дәлелденді.
2) 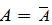 болсын, онда
болсын, онда 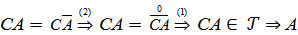 тұйық жиын. (дәлелденді)
тұйық жиын. (дәлелденді)
6. Ішкі топологиялық кеңістік.
А - (Х,  топологиялық кеңістікке ішкі жиын болсын.
топологиялық кеңістікке ішкі жиын болсын. 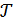 жиынның элементтерінің А жиынның қимасының жиының Т делік, яғни
жиынның элементтерінің А жиынның қимасының жиының Т делік, яғни
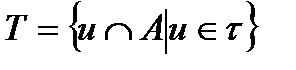 бұл жиын А жиынның ішкі жиынының тобы. Осылайша құралған Т жиыны үшін I, II, III аксиомалары орындалады, яғни
бұл жиын А жиынның ішкі жиынының тобы. Осылайша құралған Т жиыны үшін I, II, III аксиомалары орындалады, яғни
I.
II. I тобының элементтерінің кез келген жиынның бірігуі Т жиынына тиісті.
III. I жиынның элементтерінің саны шекті тобының қимасы I жиынға тиісті олай болса (А,Т) қосы топологиялық кеңістік.
Осы топологиялық кеңістікті (Х,  кеңістігінің ішкі кеңістігі деп аталады.
кеңістігінің ішкі кеңістігі деп аталады.
7. Үздіксіз бейнелеу. Гомеоморфизм.
а) Бейнелеудің үздіксіздігі. (Х,  және
және 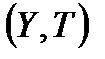 топологиялық кеңістігі берілсін.
топологиялық кеңістігі берілсін.
Ан. 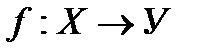
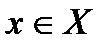 нүктесінде үздіксіз деп аталады, егерf(x) нүктесінің
нүктесінде үздіксіз деп аталады, егерf(x) нүктесінің 
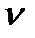 маңайы үшін, х нүктесінің
маңайы үшін, х нүктесінің 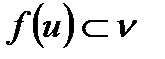 болатындай u маңайы табылса, f бейнелеуі Х жиынында үздіксіз деп аталады, егер ол Х жиынының әрбір нүктесінде үздіксіз болса.
болатындай u маңайы табылса, f бейнелеуі Х жиынында үздіксіз деп аталады, егер ол Х жиынының әрбір нүктесінде үздіксіз болса.
Теорема. (Х,  және
және 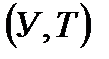 көшіретін f бейнелеуі үздіксіз болу үшін Y жиынның
көшіретін f бейнелеуі үздіксіз болу үшін Y жиынның  ашық ішкі бөлігінің прообрразы Х жиынның ашық жиыны болса
ашық ішкі бөлігінің прообрразы Х жиынның ашық жиыны болса 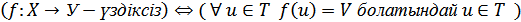
Дәледеуі: 1) (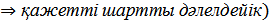
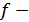 үздіксіз бейнелеу.
үздіксіз бейнелеу. 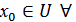 нүкте алайық.
нүкте алайық. 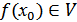 болғандықтан
болғандықтан 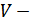
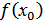 нүктесінің маңайы. Теорема шарты бойынша
нүктесінің маңайы. Теорема шарты бойынша 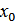 нүктесінде
нүктесінде 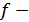 үздіксіз, сондықтан
үздіксіз, сондықтан 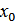 нүктесінің
нүктесінің 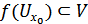 болатындай
болатындай 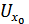 маңайы табылады және
маңайы табылады және 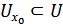 болады. Яғни
болады. Яғни 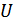 жиыны
жиыны 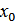 нүктесімен қатар оның
нүктесімен қатар оның 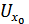 маңайын да қамтиды, ал мұндай жиын анықтама бойынша ашық жиын болады, сондықтан
маңайын да қамтиды, ал мұндай жиын анықтама бойынша ашық жиын болады, сондықтан 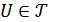 (
(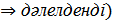
2) Айталық 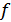 бейнелеуінде
бейнелеуінде 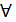 ашық жиынның прообразы ашық жиын болсын.
ашық жиынның прообразы ашық жиын болсын. 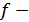 үздіксіз бейнелеу екенін дәлелдейік, яғни
үздіксіз бейнелеу екенін дәлелдейік, яғни 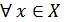 нүктесінде
нүктесінде 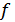 үздіксіз екенін дәлелдейік.
үздіксіз екенін дәлелдейік.
Кейбір 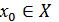 нүктесін және
нүктесін және 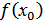 нүктесінің
нүктесінің 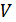 маңайын алайық.Теореманың шарты бойынша
маңайын алайық.Теореманың шарты бойынша 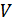 жиынының прообразы
жиынының прообразы 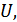 Х жиынында ашық жиын. Сонымен
Х жиынында ашық жиын. Сонымен 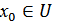 және
және 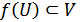 болатындай
болатындай 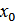 нүктесінің
нүктесінің 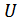 маңайы табылды. Ал бұдан
маңайы табылды. Ал бұдан 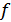 бейнелеуі
бейнелеуі 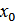 нүктесінде үздіксіз болатыны шығады. Теорема толық дәлелденді.
нүктесінде үздіксіз болатыны шығады. Теорема толық дәлелденді.
б) Гомеоморфизм.
Ан. 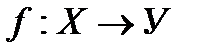 бейнелеуі гомеоморфизм (немесе топологиялық бейнелеу) деп аталады, егер ол өзара бірмәнді және өзара үздіксіз болса,
бейнелеуі гомеоморфизм (немесе топологиялық бейнелеу) деп аталады, егер ол өзара бірмәнді және өзара үздіксіз болса,
(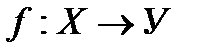 гомеоморфизм)
гомеоморфизм) 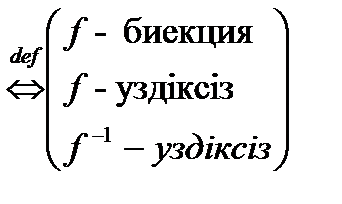
Егер 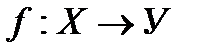 гомеоморфизм болса, онда Х,У кеңістіктері өзара гомеоморфты деп аталады және
гомеоморфизм болса, онда Х,У кеңістіктері өзара гомеоморфты деп аталады және 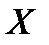 ~У түрінде белгіленеді. Сонымен топологиялық кеңістіктер класында (оны М делік) ~ қатынасын алдық. Бұл қатынас (~) эквиваленті болады, яғни рефлексивті, транзитивті және симметриялы.
~У түрінде белгіленеді. Сонымен топологиялық кеңістіктер класында (оны М делік) ~ қатынасын алдық. Бұл қатынас (~) эквиваленті болады, яғни рефлексивті, транзитивті және симметриялы.
Ан. 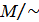 фактор жиынның элементтері топологиялық кеңістік типі деп аталады.
фактор жиынның элементтері топологиялық кеңістік типі деп аталады.
Ан. Гомеоморфты екі кеңістік топологиялық эквивалентті немесе бір топологиялық типті кеңістіктер деп аталады.
Ан. (Х,  кеңістігінің гомеоморфизмде өзгермейтін қасиеттері топологиялық қасиеттер деп аталады осындай қасиеттерді оқытатын математикалық бөлігін топология деп аталады.
кеңістігінің гомеоморфизмде өзгермейтін қасиеттері топологиялық қасиеттер деп аталады осындай қасиеттерді оқытатын математикалық бөлігін топология деп аталады.
в) Гомеоморфты жиындардын мысалдары.
1. 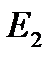 евклидтік жазықтығында ұштары А және В нүктелері болатын
евклидтік жазықтығында ұштары А және В нүктелері болатын 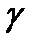 жарты шеңберін және ұштары
жарты шеңберін және ұштары 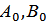 - А және В нүктелерінің шеңберге АВ түзуіне параллель жанамадағы ортогональ проекциялары болатын
- А және В нүктелерінің шеңберге АВ түзуіне параллель жанамадағы ортогональ проекциялары болатын 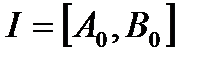 кесіндісін қарастырамыз.
кесіндісін қарастырамыз.
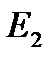 евклидтік жазықтықтың топологиясы
евклидтік жазықтықтың топологиясы 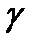 жиында кейбір
жиында кейбір 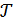 топологиясын, ал
топологиясын, ал 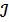 жиынында Т топологиясын индуциялайды (анықтайды), яғни (
жиынында Т топологиясын индуциялайды (анықтайды), яғни (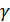 ,
,  , (У, Т) топологиясы ішкі кеңістіктер болады. Олар гомеоморфты.
, (У, Т) топологиясы ішкі кеңістіктер болады. Олар гомеоморфты.
Шынында да, айталық 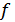 -
- 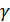 жарты шеңберін
жарты шеңберін 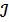 кесіндісіне ортогональ проекциялау болсын.
кесіндісіне ортогональ проекциялау болсын.
1. f - өзара бірмәнді екені айқын.
2. f – үздіксіз екенін көрсетейік. Ол үшін 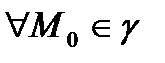 нүктесін және оның образы
нүктесін және оның образы 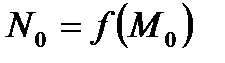 нүктесін қарастырамыз.
нүктесін қарастырамыз. 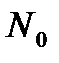 нүктесінің
нүктесінің 
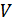 маңайы үшін
маңайы үшін 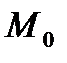 нүктесінің
нүктесінің 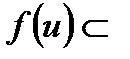
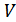 болатындай u маңайын көрсетуге болады. Бұдан
болатындай u маңайын көрсетуге болады. Бұдан 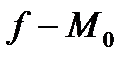 нүктесінде үздіксіз екенің көреміз, ал
нүктесінде үздіксіз екенің көреміз, ал 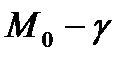 шеңберінің кез келген нүктесі болғандықтан
шеңберінің кез келген нүктесі болғандықтан 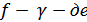 үздіксіз екені шығады.
үздіксіз екені шығады.
Сонымен қатар 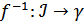 кері бейнелеуі де үздіксіз болады. Олай болса
кері бейнелеуі де үздіксіз болады. Олай болса
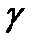 ~
~ 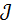 .(дәлелденді)
.(дәлелденді)
2 мысал. 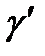 - ұштарынсыз жарты шеңбер
- ұштарынсыз жарты шеңбер 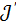 ұштарының
ұштарының 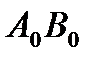 кесіндісі
кесіндісі
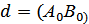 түзуі болсын.
түзуі болсын. 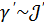 екенін көреміз.
екенін көреміз.
3 мысал. 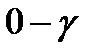 жарты шеңбердің центрі болсын.
жарты шеңбердің центрі болсын.
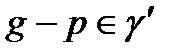 нүктесін
нүктесін 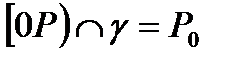 болатын нүктелеріне
болатын нүктелеріне 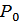 бейнелеу болсын.
бейнелеу болсын.
g – гомеоморфизм болады.
4 мысал. 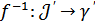 ,
, 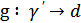
гомеоморфизмдерінің композициясы да гомеоморфизм болатыны белгілі, сондықтан g 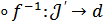
Олай болса ұшсыз кесінді түзуге гомеоморфты. Бұдан (а,в) сан интервалы 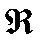 жиынына гомеоморфты екені шығады. Осындай салулардан төмендегі тұжырымдарды аламыз:
жиынына гомеоморфты екені шығады. Осындай салулардан төмендегі тұжырымдарды аламыз:
 Шетті жарты сфера тұйық дөңгелекке гомеоморфты.
Шетті жарты сфера тұйық дөңгелекке гомеоморфты.
 Ашық (шетсіз) дөңгелек жазықтыққа гомеоморфты.
Ашық (шетсіз) дөңгелек жазықтыққа гомеоморфты.
 Шетсіз жарты сфера ашық дөңгелекке гомеоморфты.
Шетсіз жарты сфера ашық дөңгелекке гомеоморфты.
 Дөңес көпбұрыш тұйық дөңгелекке гомеоморфты.
Дөңес көпбұрыш тұйық дөңгелекке гомеоморфты.
 Сәуле жарты интервалға гомеоморфты.
Сәуле жарты интервалға гомеоморфты.
Мысалдар. 1) 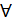 (а,в) және (с,d) интервалдары гомеоморфты, себебі
(а,в) және (с,d) интервалдары гомеоморфты, себебі 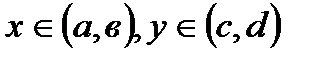 десек,
десек,
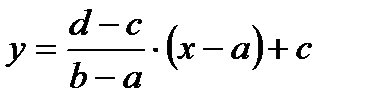
2) (а,в) интервалы 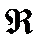 сан осі гомеоморфты
сан осі гомеоморфты
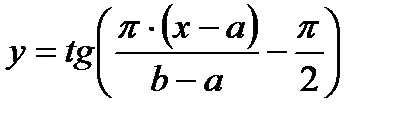
3) Сфера - кубтың бетіне гомеоморфты.
4) Бір нүктесінсіз сфера жазықтыққа гомеоморфты. Гомеоморфизмді «тесілген» нүктеден осы нүктеге диаметральді нүктеден жанасатын жазықтыққа проекциялау арқылы орнатамыз.
Анықтама. Егер 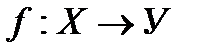 гомеоморфизм және
гомеоморфизм және 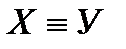 болса, онда
болса, онда 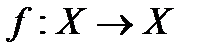 бейнелеуі Х кеңістігінде гомеоморфизмі деп аталады.
бейнелеуі Х кеңістігінде гомеоморфизмі деп аталады.
г) Гомеоморфизмнің қарапайым қасиеттері.
Теорема.  топологиялық кеңістікті өзіне өзін теңбе – тең бейнелеу гомеоморфизм болады.
топологиялық кеңістікті өзіне өзін теңбе – тең бейнелеу гомеоморфизм болады.
Теорема. Гомеоморфизмге кері бейнелеу гомеоморфизм болады.
Теорема. Екі гомеоморфизмнің композициясы гомеоморфизм болады.
Дәлелдеуі: 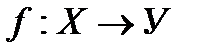 , g:
, g: 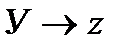 гомеоморфизм
гомеоморфизм 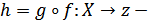 үздіксіз, себебі
үздіксіз, себебі 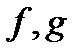 - үздіксіз,
- үздіксіз, 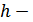 биекция (
биекция (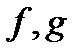 - биекция, )
- биекция, ) 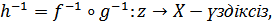 себебі
себебі 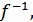
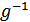 -
- 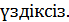 Олай болса,
Олай болса, 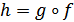 – гомеоморфизм. Теорема дәлелденді
– гомеоморфизм. Теорема дәлелденді
8. Топологиялық кеңістіктердің кластары.
Ан. (Байланысты топологиялық кеңістіктің анықтамасы). Х топологиялық кеңістігінде 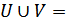 X,
X, 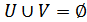 теңдіктері орындалатын құр емес екі
теңдіктері орындалатын құр емес екі 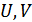 ашық жиындары табылса, яғни Х жиыны ортақ нүктесі жоқ құр емес екі ашық жиынға бөлінген болса, онда Х жиыны байланыссыз деп аталады. Егер мұндай бөліну мүмкін болмаса, онда Х байланысты жиын деп аталады.
ашық жиындары табылса, яғни Х жиыны ортақ нүктесі жоқ құр емес екі ашық жиынға бөлінген болса, онда Х жиыны байланыссыз деп аталады. Егер мұндай бөліну мүмкін болмаса, онда Х байланысты жиын деп аталады.
Мысалы, R байланысты жиын. Себебі 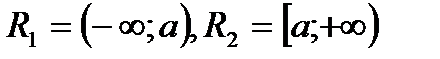
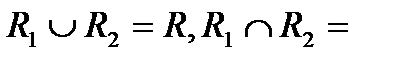 Ø бірақ
Ø бірақ 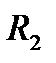 ашық емес жиын.
ашық емес жиын.
Байланысты жиынның басқа анықтамасын берейік.
Ан. Құр емес екі тұйық жиынға бөлінбейтін топологиялық кеңістік байланысты деп аталады.
Мысал, 1) 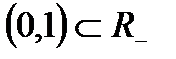 байланысты жиын.
байланысты жиын.
2) 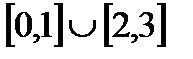 байланыссыз жиын.
байланыссыз жиын.
3) N – байланыссыз жиын.
Хаусдорфты топологиялық кеңістік.
Ан. (ажырайтын топологиялық кеңістік анықтамасы). Егер Х топологиялық кеңістіктің әртүрлі нүктелерінің қиылспайтын маңайлары бар болса, онда Х ажырайтын не хаусдорфты топологиялық кеңістік деп аталады.
Ф.Хаусдорф – 1-ші болып топологиялық кеңістік ұғымын еңгізген неміс математигі.
(X - хаусдорфты) 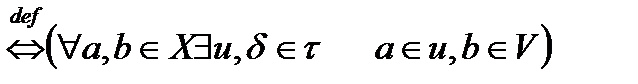
Мысал..  Евклид кеңістігі, барлық метрикалақ кеңістік ажырайтын топологиялық кеңістікболады.
Евклид кеңістігі, барлық метрикалақ кеңістік ажырайтын топологиялық кеңістікболады.
Ан. Жиынның бүркемесі (покрытие). Х жиынның бүркемесі деп оның бірігуі Х жиынның өзі болатындай 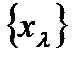 ішкі жиындардың тобын айтады.
ішкі жиындардың тобын айтады.
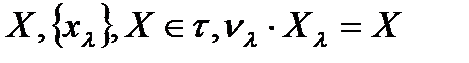
Ан. (Х,  топологиялық кеңістігінің (
топологиялық кеңістігінің (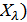 бүркемесі ашық жиын деп аталады, егер әрбір
бүркемесі ашық жиын деп аталады, егер әрбір 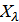 ашық жиын болса.
ашық жиын болса.
Ан. (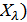 бүркемесінің ішкі бүркемесі деп оның өзі бүркеме болатындай ішкі тобын айтады.
бүркемесінің ішкі бүркемесі деп оның өзі бүркеме болатындай ішкі тобын айтады.
Ан. (компактілі) топологиялық кеңістік (Х,  топологиялық компактілі деп аталады, егер оның әрбір ашық бүркемесі саны шекті ішкі бүркемелерден құралатын болса.
топологиялық компактілі деп аталады, егер оның әрбір ашық бүркемесі саны шекті ішкі бүркемелерден құралатын болса.
Ан. (Х,  топологиялық кеңістігінің А жиыны компактісі деп аталады, егер А ішкі кеңістігі компактілі болса.
топологиялық кеңістігінің А жиыны компактісі деп аталады, егер А ішкі кеңістігі компактілі болса.
Ан. Х жиынның бүркемесі осы жиынның бөліктеуі (разбиение) деп аталады, егер бүркеменің элементтері құр емес жиындар және әрбір әртүрлі екі элементі қиылыспайтын болса.
Ескерту. Топологиялық кеңістіктің ажырайтын байланысты, компактілі болуы гомеоморфизмде сақталады. Мысалы, байланысты жиынға гомеоморфты жиын байланысты болады.
§2. Евклидтік кеңстіктегі сызықтар.
1. Скаляр аргументтің вектор функциясы.
Анықтама. Геометриялық фигуралардың қасиеттерін математикалық анализдің әдістерін пайдаланып, оқытатын геометрияның бөлімі дифференциалдық геометрия деп аталады.
1. Вектор функцияның анықтамасы, шегі, үздіксіздік ұғымы, туындысы.
Анықтама. V – үш өлшемді Евклидтік векторлық кеңістік I – кейбір сан аралығы болсын. Егер 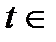 I санына қандай да бір заңдылық бойынша V кеңістігінің
I санына қандай да бір заңдылық бойынша V кеңістігінің 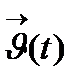 векторы сәйкес келсе, онда I аралығында скаляр t аргументтің
векторы сәйкес келсе, онда I аралығында скаляр t аргументтің 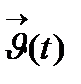 функциясы берілген делінеді.
функциясы берілген делінеді. 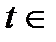 I,
I, 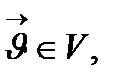
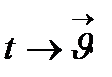
Анықтама. I аралығында анықталған 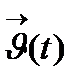 функциясы
функциясы 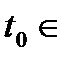 I нүктесінің маңайында ақырсыз аз функция деп аталады, егер
I нүктесінің маңайында ақырсыз аз функция деп аталады, егер 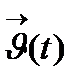 функциясы осы нүктенің маңайында ақырсыз аз функция болса.
функциясы осы нүктенің маңайында ақырсыз аз функция болса. 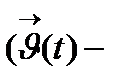 t нүктесінің маңайында ақырсыз аз функция)
t нүктесінің маңайында ақырсыз аз функция) 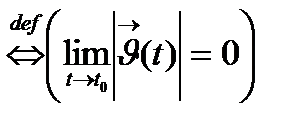
Анықтама. 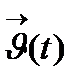 функциясының
функциясының 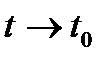 ұмтылғандағы шегі деп
ұмтылғандағы шегі деп 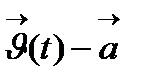 функциясы ақырсыз аз функция болатындай а тұрақты векторын айтады және
функциясы ақырсыз аз функция болатындай а тұрақты векторын айтады және 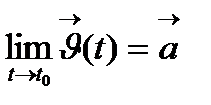 түрінде жазылады.
түрінде жазылады. 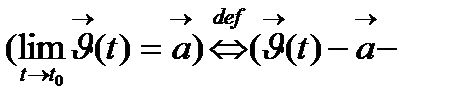 ақырсыз аз функция)
ақырсыз аз функция)
Анықтама. Егер 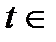 I нүктесінде
I нүктесінде 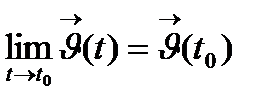 болса, онда
болса, онда 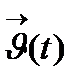 функциясы
функциясы 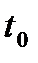 нүктесінде үздіксіз деп аталады.
нүктесінде үздіксіз деп аталады.
Анықтама. 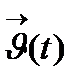 функциясы I аралығының кез келген нүктесінде үздіксіз болса, онда бұл функция I аралығында үздіксіз деп аталады.
функциясы I аралығының кез келген нүктесінде үздіксіз болса, онда бұл функция I аралығында үздіксіз деп аталады.
Анықтама. 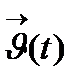 функциясы I аралығында берілген.
функциясы I аралығында берілген. 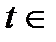 I нүктесінде t аргументіне өсімше
I нүктесінде t аргументіне өсімше 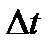 –ны берейік. Сонда функция
–ны берейік. Сонда функция 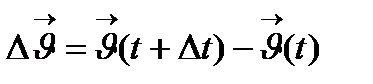 өсімшесін қабылдады. Егер
өсімшесін қабылдады. Егер 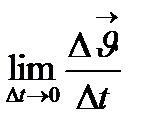 шегі бар болса, осы шекті
шегі бар болса, осы шекті 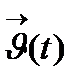 функциясының t нүктесіндегі туындысы деп аталады және
функциясының t нүктесіндегі туындысы деп аталады және 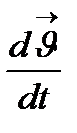 немесе
немесе 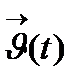 түрінде белгіленеді.
түрінде белгіленеді. 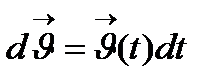 векторы
векторы 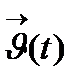 функциясының дифференциалы деп аталады. Егер
функциясының дифференциалы деп аталады. Егер 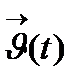 функциясының I аралығының әрбір нүктесінде туындысы бар болса, бұл функция I аралығында дифференциалданады дейді.
функциясының I аралығының әрбір нүктесінде туындысы бар болса, бұл функция I аралығында дифференциалданады дейді.
2. Вектор функцияның координаттар ұғымы.
V векторлық кеңістігінде ортонормаланған 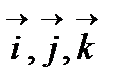 базисі берілген.
базисі берілген. 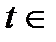 I нүктесінде
I нүктесінде 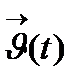 векторын
векторын 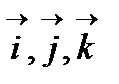 базис векторлары бойынша жіктейік:
базис векторлары бойынша жіктейік:
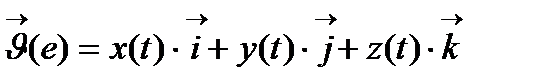 (1)
(1)
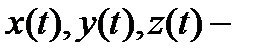 скаляр функциялар, олар
скаляр функциялар, олар 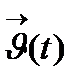 функциясының
функциясының 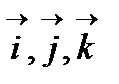 базисіндегі координаталары деп аталады.
базисіндегі координаталары деп аталады.
Вектор функцияның координаталары ұғымын негізгеннен кейін, үздіксіздік, шек ұғымына қатысты мына тұжырымдарды айтуға болады:
1) 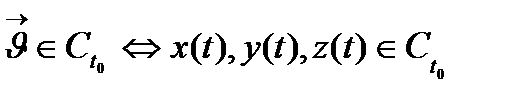 (t0 нүктесінде үздіксіз)
(t0 нүктесінде үздіксіз)
2) Егер 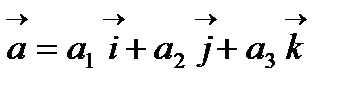 берілсе, онда
берілсе, онда
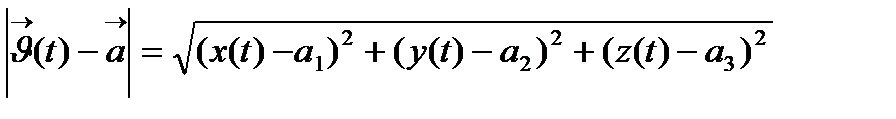 формуласынан
формуласынан 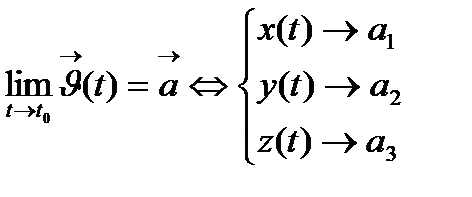
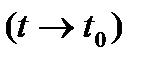
3) Теорема. (1) теңдігі бойынша жіктелген функциясы аралығында дифференциалдану үшін функцияларының аралығында дифференциалдануы қажетті және жеткілікті.
3. Вектор функцияның дифференциалдау ережелері:
· 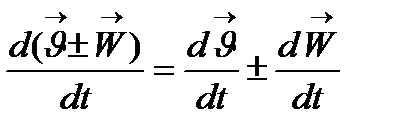
· 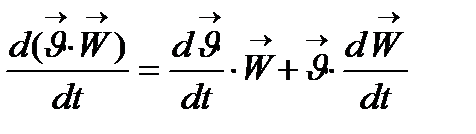
· 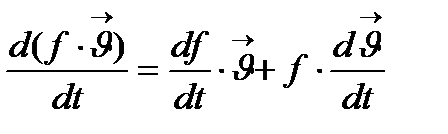
· 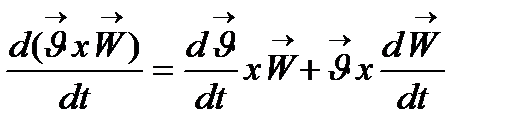
Лемма: Егер I аралығында 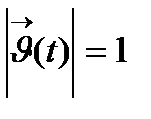 болса, онда
болса, онда 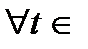 I үшін
I үшін 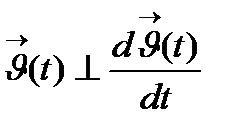 орындалады. немесе
орындалады. немесе 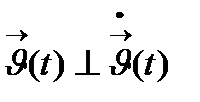
Ескерту: 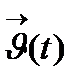 функциясының
функциясының 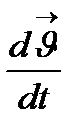 туындысы да t айнымалысынан тәуелді функция болады (I аралығында). Сондықтан жоғары ретті туынды ұғымы енгізіледі.
туындысы да t айнымалысынан тәуелді функция болады (I аралығында). Сондықтан жоғары ретті туынды ұғымы енгізіледі. 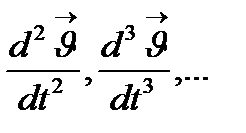
§ 3 Сызық ұғымы
1. Сызық туралы түсінік.
Сызық туралы бастапқы түсінік қозғалыстағы нүктенің траекториясын елестету арқылы немесе сымды, жіпті елестету арқылы пайда болады. Сызықтың математикалық анықтамасы бастапқы түсінікті абстрактылаудың нәтижесі болып табылады.
М нүктесі Е3 евклид кеңістігінде қозғалсын, 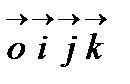 тік бұрышты координат жүйесі берілсін, I кейбір уақыт аралығы болсын.
тік бұрышты координат жүйесі берілсін, I кейбір уақыт аралығы болсын.
 М нүктесінің t
М нүктесінің t 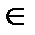 I уақыт мезгіліндегі орнын
I уақыт мезгіліндегі орнын 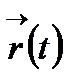 вектор функциясы мен анықтауға болады, t айнымалысы I аралығында өзгергенде осы аралықта анықталған
вектор функциясы мен анықтауға болады, t айнымалысы I аралығында өзгергенде осы аралықта анықталған 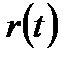 функциясын аламыз.
функциясын аламыз.
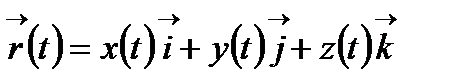 (1)
(1)
және теңдігі дұрыс болады. Осы теңдік n нүктесінің 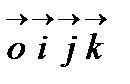 жүйесіндегі қозғалыс заңы деп атайды. t уақытты I аралығында өзгергенде m нүктесі кеңістікте кейбір траектория сызады.
жүйесіндегі қозғалыс заңы деп атайды. t уақытты I аралығында өзгергенде m нүктесі кеңістікте кейбір траектория сызады.
| Z |
| X |
| Y |
| M |
| g |
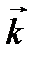 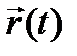
|
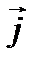
|
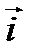
|
2. Элементар сызық.
Анықтама. Е3 евклид кеңістігіндегі түзуді кесіндіні сәулені қарапайым
сызық деп атайды.
Анықтама. Е3 кеңістігінің қарапайым сызықты гомеоморфты 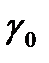 фигурасын
фигурасын
элементар сызық деп атайды, кесіндіге гомеоморфты сызықты
доға деп атайды.
Кез келген сан аралығы қарапайым сызықтардың әрқайсысына гомеоморфтылық қатынас эквивалентті екені белгілі, сондықтан элементар сызықтың анықтамасын былайша беруге болады.
Анықтама. Кейбір сан аралығына гомеоморфты 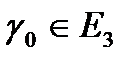 фигурасы элементар сызық деп атайды.
фигурасы элементар сызық деп атайды.
 2015-05-05
2015-05-05 2405
2405







