1. Шеңберді екі жарты шеңбер мен бүркеуге болады, ал жарты шеңбер элементар сызық олай болса шеңбер сызық болады.
2. Тангенсоиды - әрқайсысы сан интервалына гомеоморфты элементар сызықтардың есепті жиыны сондықтан тангенсоиды сызық болады.
§4. Тегіс сызық.
1. Тегіс сызық ұғымы.
Айталық, 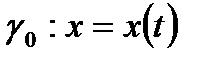 ,
, 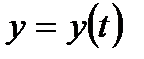 ,
, 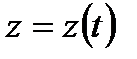 ,
, 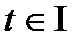 (1) эл
(1) эл  ементар сызығы берілсін.
ементар сызығы берілсін.
Анықтама: 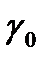 сызығы
сызығы 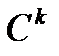 класының тегіс сызығы деп аталады, егер
класының тегіс сызығы деп аталады, егер 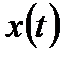 ,
, 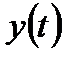 ,
, 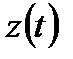 функциялары
функциялары 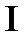 аралығында
аралығында 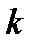 ретке дейінгі үздіксіз туындылары бар және
ретке дейінгі үздіксіз туындылары бар және 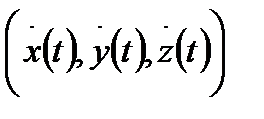 (2) матрицасының рангісі 1-ге тең болса, онда
(2) матрицасының рангісі 1-ге тең болса, онда 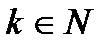 .
.
(2) шарт 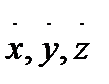 туындылары ешбір
туындылары ешбір 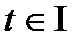 мәнінде бәрі бірдей нөлге тең емес дегенді білдіреді.
мәнінде бәрі бірдей нөлге тең емес дегенді білдіреді.
Мысал. 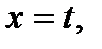
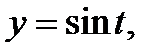
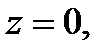
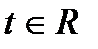 теңдеулері синусоиданы анықтайды. Бұл теңдеулердің оң бөліктері кезкелген ретті үздіксіз туындылары бар және
теңдеулері синусоиданы анықтайды. Бұл теңдеулердің оң бөліктері кезкелген ретті үздіксіз туындылары бар және 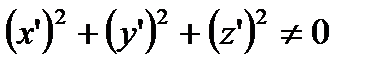 . Олай болса синусоида
. Олай болса синусоида 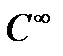 класының тегіс сызығы.
класының тегіс сызығы.
Анықтама: 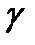 жай сызығы
жай сызығы 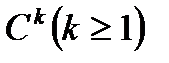 класының тегіс сызығы деп аталады, егер әрбір кезкелген ішкі
класының тегіс сызығы деп аталады, егер әрбір кезкелген ішкі 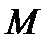 нүктесінің
нүктесінің 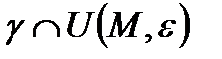 қимасы
қимасы 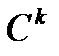 класының тегіс элементар сызығы болатындай
класының тегіс элементар сызығы болатындай 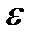 маңайы табылса.
маңайы табылса.
2.Бөлік – тегіс сызық ұғымы.
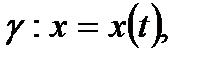
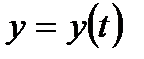 ,
, 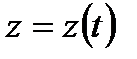 ,
,  (1)
(1)
Анықтама: Егер 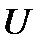 облысын әрқайсысында (1) теңдеулер тегіс сызықты анықтайтындай
облысын әрқайсысында (1) теңдеулер тегіс сызықты анықтайтындай 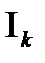 аралықтарының шекті немесе есепті жиынымен бүркеу мүмкін болса, онда
аралықтарының шекті немесе есепті жиынымен бүркеу мүмкін болса, онда 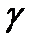 сызығы бөлік – тегіс сызық деп аталады. (
сызығы бөлік – тегіс сызық деп аталады. (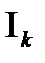 аралықтарының шеткі нүктелерінде тегістік талабы орындалмауы мүмкін)
аралықтарының шеткі нүктелерінде тегістік талабы орындалмауы мүмкін)
Мысал. 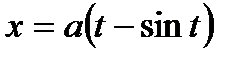 ,
, 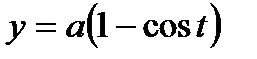 ,
, 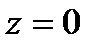 ,
, 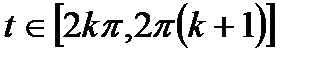 ,
,  (
(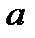 - тұрақты сан),
- тұрақты сан),
 x x
|
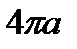
|
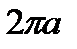
|
| y |
теңдеулерімен анықталатын фигура циклоида деп аталады. Циклоида түзуге гомеоморфты, яғни элементар сызық. Бірақ ол тегіс сызық емес.
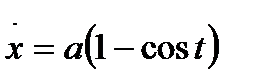 ,
, 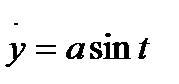 ,
, 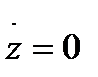 туындылары
туындылары 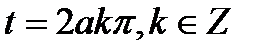 нүктелерінде
нүктелерінде 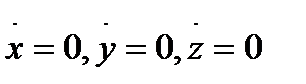 . Бұдан рангі
. Бұдан рангі 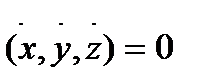 , яғни тегістік шарттың біреуі бұзылады. Олай болса циклоида тегіс сызық емес. Циклоида барлық сан түзуінде анықталғанын көреміз. Ал сан түзуін
, яғни тегістік шарттың біреуі бұзылады. Олай болса циклоида тегіс сызық емес. Циклоида барлық сан түзуінде анықталғанын көреміз. Ал сан түзуін 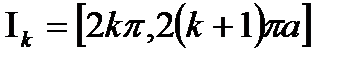 аралықтарының саналатын жиынмен бүркеуге болады. Ал
аралықтарының саналатын жиынмен бүркеуге болады. Ал 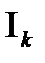 аралықтарының әрқайсысында берілген теңдеулер тегіс сызықты анықтайды. Олай болса, циклоида бөлік - тегіс сызық.
аралықтарының әрқайсысында берілген теңдеулер тегіс сызықты анықтайды. Олай болса, циклоида бөлік - тегіс сызық.
§5. Қисыққа жанама
1. Қисыққа жүргізілген жанаманың анықталған жанаманың бар болуы туралы теорема.
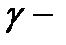 сызығы,
сызығы, 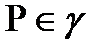 нүктесі,
нүктесі, 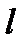 түзуі
түзуі 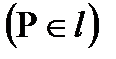 берілсін.
берілсін.
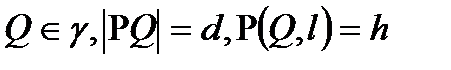 болсын.
болсын.
Анықтама. 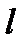 түзуі
түзуі 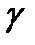 сызығының
сызығының 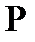 нүктесінде жүргізілген жанама деп аталады, егер
нүктесінде жүргізілген жанама деп аталады, егер 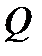 нүктесі қисық бойымен
нүктесі қисық бойымен 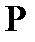 нүктесіне шексіз жақындағанда
нүктесіне шексіз жақындағанда 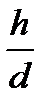 бөлшегі 0-ге ұмтылса.
бөлшегі 0-ге ұмтылса.
|
Теорема. 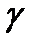 тегіс сызықтың әрбір нүктесінде жанама болады және ол біреу болады. Егер
тегіс сызықтың әрбір нүктесінде жанама болады және ол біреу болады. Егер 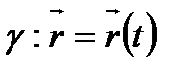 векторлық теңдеуімен берілсе, онда
векторлық теңдеуімен берілсе, онда 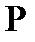 нүктесіндегі жанаманың бағыты параметрдің осы нүктеге сәйкес мәніндегі
нүктесіндегі жанаманың бағыты параметрдің осы нүктеге сәйкес мәніндегі 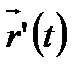 векторының бағытымн анықталады, яғни жанама
векторының бағытымн анықталады, яғни жанама 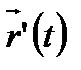 векторына параллель болады.
векторына параллель болады.
Дәлелдеуі: Айталық параметрдің 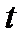 мәніне сәйкес
мәніне сәйкес 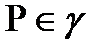 нүктесінде
нүктесінде 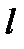 түзуі
түзуі 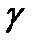 сызығына жанама болсын.
сызығына жанама болсын. 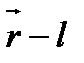 түзуінің бағыттаушы бірлік векторы болсын.
түзуінің бағыттаушы бірлік векторы болсын.
Параметрдің 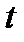 мәніне
мәніне 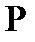 нүктесі, ал
нүктесі, ал 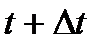 мәніне
мәніне 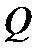 нүктесі сәйкес келсін.
нүктесі сәйкес келсін.
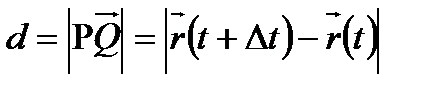
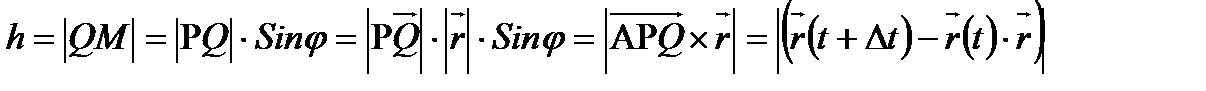
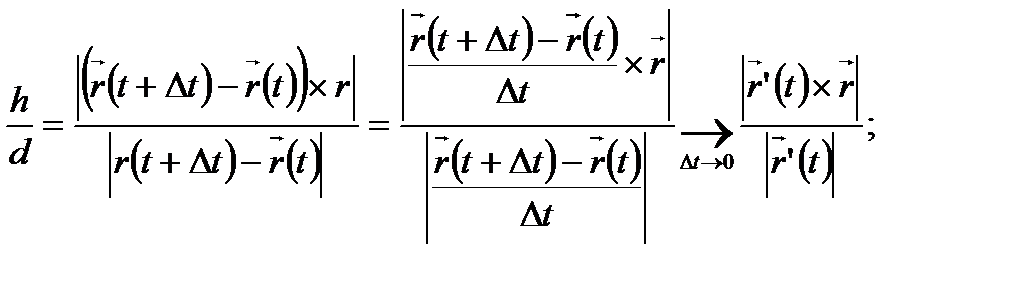
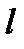 түзуі
түзуі 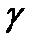 сызығына
сызығына 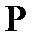 нүктесінде жүргізілген жанама болғандықтан
нүктесінде жүргізілген жанама болғандықтан 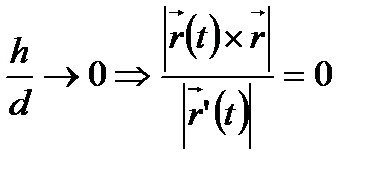 болады, яғни
болады, яғни 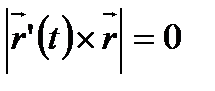 , ал бұл теңдік тек
, ал бұл теңдік тек 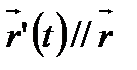 болғанда ғана мүмкін. Сонымен, егер
болғанда ғана мүмкін. Сонымен, егер 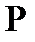 нүктесінде жанама бар болса,
нүктесінде жанама бар болса, 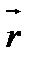 векторы оның бағыттаушы векторы болады, бұдан жанаманың біреуі екені шығады.
векторы оның бағыттаушы векторы болады, бұдан жанаманың біреуі екені шығады. 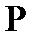 нүктесі арқылы өтетін,
нүктесі арқылы өтетін, 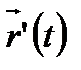 векторына параллель
векторына параллель 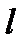 түзуі
түзуі 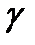 сызығына жанама болатыныда дұрыс, себебі
сызығына жанама болатыныда дұрыс, себебі
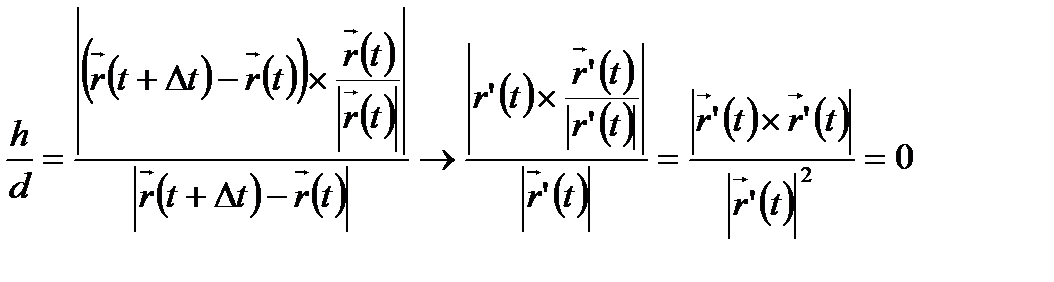 , яғни
, яғни 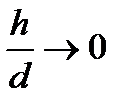
2. Жанаманың әртүрлі теңдеулері
1) 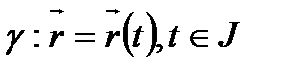 берілсе, жанаманың векторының теңдеуі
берілсе, жанаманың векторының теңдеуі 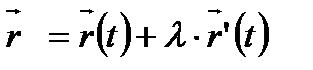 (1) түрінде болады.
(1) түрінде болады.
2) 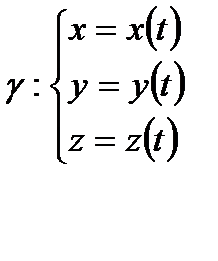
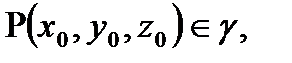
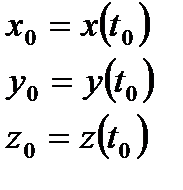
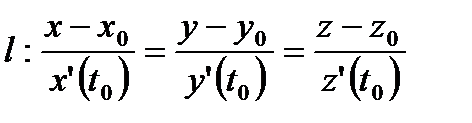 (2)
(2)
3) 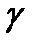 -
- 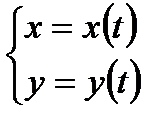
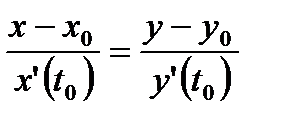 (3)
(3)
4) 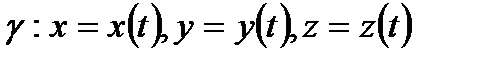
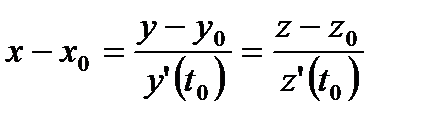 (4)
(4)
5) 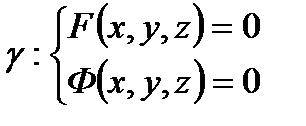 сызық теңдеулерімен берілсін.
сызық теңдеулерімен берілсін.
Жанаманың теңдеуін жазу керек.
Айдалық 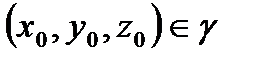 нүктесінің маңайын
нүктесінің маңайын 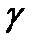 сызығы
сызығы 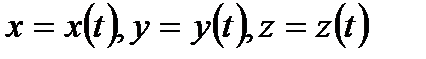 параметрлік теңдеулерімен анықталсын. Бұл жағдайда жанаманың теңдеуін жазу үшін
параметрлік теңдеулерімен анықталсын. Бұл жағдайда жанаманың теңдеуін жазу үшін 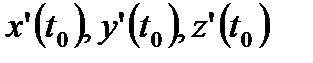 туынды мәндерін табу жеткілікті.
туынды мәндерін табу жеткілікті.
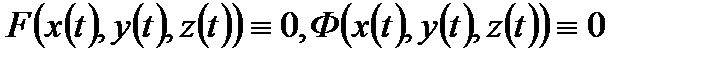 теңбе-теңдіктерін аламыз. Бұл теңдіктерді
теңбе-теңдіктерін аламыз. Бұл теңдіктерді 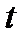 бойынша дифференциалдасақ
бойынша дифференциалдасақ 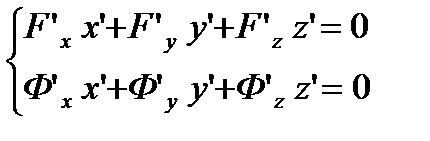 теңдіктерін аламыз.
теңдіктерін аламыз.
Бұл жүйеден 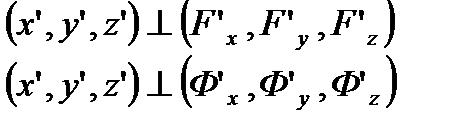 шарттарын аламыз. Олай болса,
шарттарын аламыз. Олай болса,
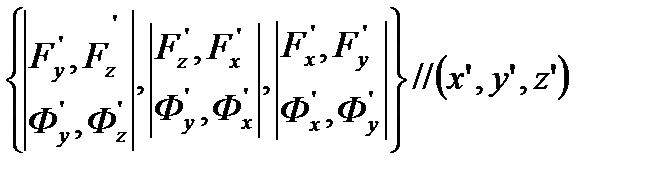 екені шығады. Олай болса, жанаманың теңдеуі
екені шығады. Олай болса, жанаманың теңдеуі 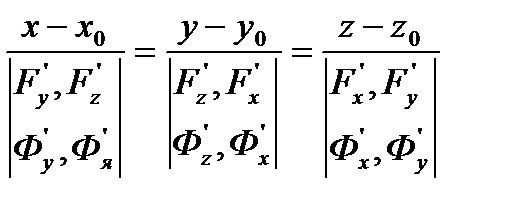 (5)
(5)
Түрінде болады.
6) 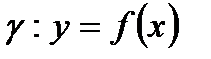 болса, жанаманың теңдеуі
болса, жанаманың теңдеуі 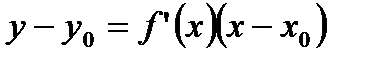 (6)
(6)
7) 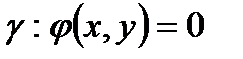
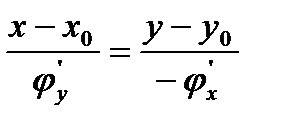 (7)
(7)
3. Нормаль жазықтық.
Анықтама. Қисықтың 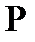 нүктесіндегі жанамасына перпендикуляр және осы нүкте арқылы өтетін жазықтық
нүктесіндегі жанамасына перпендикуляр және осы нүкте арқылы өтетін жазықтық 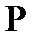 нүктесіндегі нормаль жазықтық деп аталады.
нүктесіндегі нормаль жазықтық деп аталады.
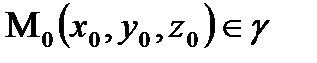 болса, нормаль жазықтықтың теңдеуі
болса, нормаль жазықтықтың теңдеуі 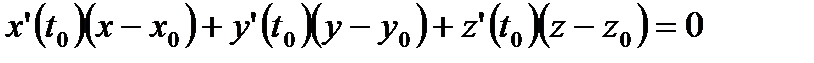 (8) түрінде болады.
(8) түрінде болады.
§6. Доғаның ұзындығы
1. 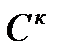 класының
класының 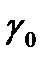 тегіс сызығы
тегіс сызығы 
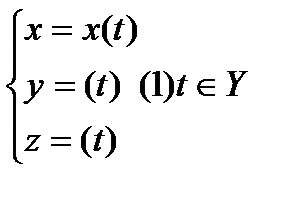 теңдеулерімен берілсін.
теңдеулерімен берілсін.
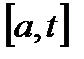 кесіндісі
кесіндісі 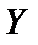 аралығының бөлігі болсын.
аралығының бөлігі болсын. 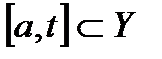
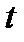 параметрі осы кесіндіде өзгергенде (1) теңдеулер
параметрі осы кесіндіде өзгергенде (1) теңдеулер 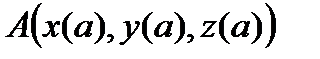


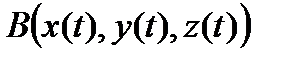 нүктелері болатын кейбір
нүктелері болатын кейбір 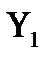 доғасын сызады.
доғасын сызады.
| A |
| B |
Матанализден бұл доғаның ұзындығы S мына формуламен есептелетіні белгілі 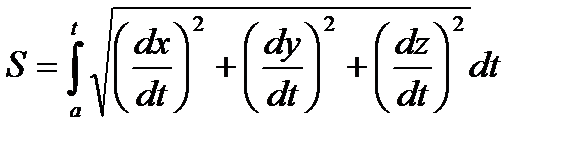 (2) немесе векторлық формада жазсақ
(2) немесе векторлық формада жазсақ 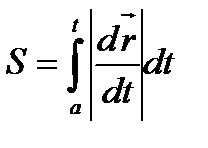 (2).
(2).
Бұл формулалардан 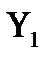 доғаның ұзындығы
доғаның ұзындығы 
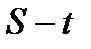 дан тәуелді функция екенін көреміз. Жоғары шегі айнымалы болатын интегралдың қасиеті бойынша
дан тәуелді функция екенін көреміз. Жоғары шегі айнымалы болатын интегралдың қасиеті бойынша 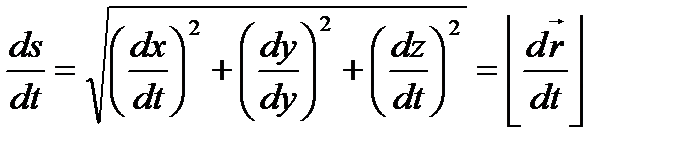 (4)
(4)
Егер 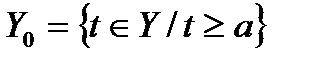 аралығында (1) функциялар кейбір
аралығында (1) функциялар кейбір 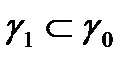 тегіс сызығын анықтайды.(2) формула
тегіс сызығын анықтайды.(2) формула 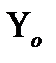 аралығын
аралығын 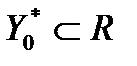 аралығына
аралығына 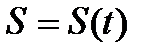 бейнелеуін орнатады. Бұл функция
бейнелеуін орнатады. Бұл функция 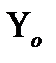 аралығында монотонды өспелі, себебі
аралығында монотонды өспелі, себебі 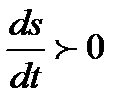 олай болса, оған кері
олай болса, оған кері 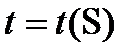 функциясы табылады, және
функциясы табылады, және 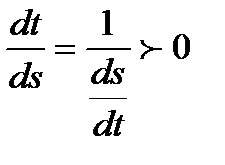 (5)
(5)
(2) формуладан 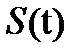 функциясы
функциясы 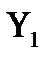 аралығында К ретке дейін үздіксіз туындысы бар екені шығады. Ал (5) формуладан
аралығында К ретке дейін үздіксіз туындысы бар екені шығады. Ал (5) формуладан 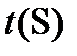 функциясының К ретке дейін үздіксіз туындылары бар екені шығады.Олай болса
функциясының К ретке дейін үздіксіз туындылары бар екені шығады.Олай болса 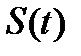 функциясы аралықтарының арасында гомоморфизм орнатады. Сондықтан, сызықтың теңдеулерінде параметр ретінде осы сызықтың кейбір нүктесінен басталатындығынан S ұзындығын алуға болады.
функциясы аралықтарының арасында гомоморфизм орнатады. Сондықтан, сызықтың теңдеулерінде параметр ретінде осы сызықтың кейбір нүктесінен басталатындығынан S ұзындығын алуға болады.
Сызықты бұлайша параметрлеу табиғи параметрлеу деп аталады.
I тегіс сызықта табиғи параметрлеу берілсін. Онда (1) теңдулер 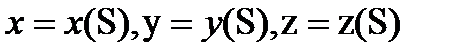 түрінде болады. Мұнда S – A нүктесінен басталатын доғаның ұзындығы.
түрінде болады. Мұнда S – A нүктесінен басталатын доғаның ұзындығы.
(2) формулада 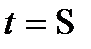 десек
десек

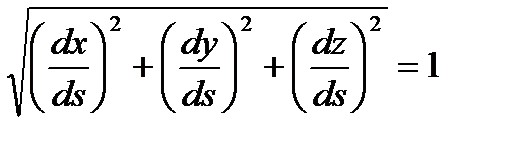 теңдеуін аламыз, яғни
теңдеуін аламыз, яғни 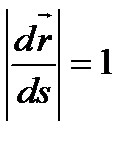 , бұдан
, бұдан 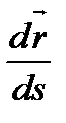 - бірлік вектор екені шығады, оны
- бірлік вектор екені шығады, оны 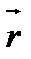 делік.
делік. 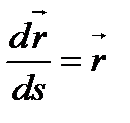 - жанаманың бірлік векторы.
- жанаманың бірлік векторы.
Мысалы: 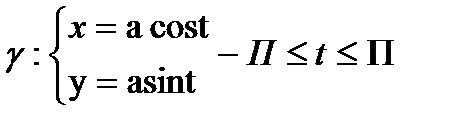
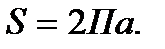
§7. Сызықтық қисықтығы және бұралуы.
1. Сызық қисықтығы, теорема.
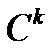
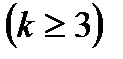 класының
класының 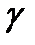 тегіс сызығы
тегіс сызығы 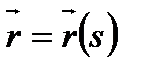 (1) немесе
(1) немесе 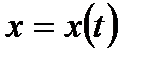 ,
, 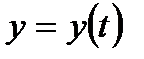 ,
, 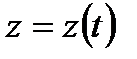 (1’) теңдеулерімен берілсін.
(1’) теңдеулерімен берілсін. 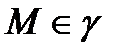 нүктесінен жүргізілген жанаманың бірлік векторы
нүктесінен жүргізілген жанаманың бірлік векторы 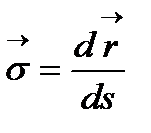 екені белгілі.
екені белгілі.
Анықтама: 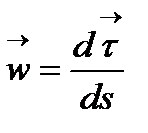 векторы
векторы 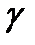 сызығының
сызығының 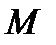 нүктесіндегі қисығының векторы деп аталады. Ал ұзындығы
нүктесіндегі қисығының векторы деп аталады. Ал ұзындығы 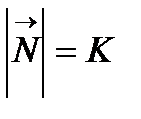 саны
саны 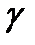 сызығының осы нүктедегі қисықтығы деп аталады.
сызығының осы нүктедегі қисықтығы деп аталады.
z
М
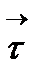
у
х
Қисықтық K- S параметрлеріне тәуелді функция.
Анықтама: Егер 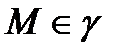 нүктесінде
нүктесінде 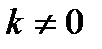 болса,
болса, 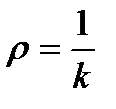 саны
саны 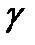 сызығының
сызығының 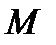 нүктесіндегі қисықтық радиусы деп аталады. Егер
нүктесіндегі қисықтық радиусы деп аталады. Егер 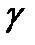 сызығы (1) теңдеумен берілсе, оның кез келген нүктесіндегі қисықтығы
сызығы (1) теңдеумен берілсе, оның кез келген нүктесіндегі қисықтығы
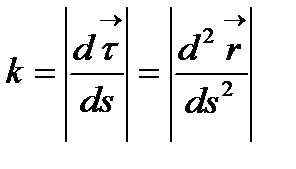 (2) формула, ал (1’) теңдеулерімен берілсе,
(2) формула, ал (1’) теңдеулерімен берілсе, 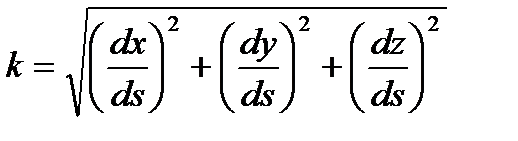 (2’) формуласымен есептеледі.
(2’) формуласымен есептеледі.
Теорема: 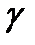 сызығы қарапайым сызық болу үшін оның әрбір нүктесіндегі қисықтығы
сызығы қарапайым сызық болу үшін оның әрбір нүктесіндегі қисықтығы
нольге тең болуы қажетті және жеткілікті.
(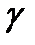 - қарапайым сызық)
- қарапайым сызық) 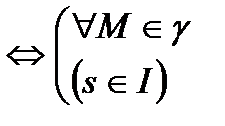
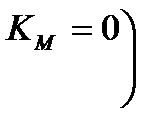
Дәлелдеуі:
1) 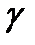 - қарапайым сызық делік, яғни түзу немесе оның бөліктері түзудің векторлық теңдеуі
- қарапайым сызық делік, яғни түзу немесе оның бөліктері түзудің векторлық теңдеуі 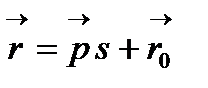 (
(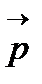 ,
, 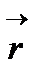 - тұрақты векторлар),
- тұрақты векторлар), 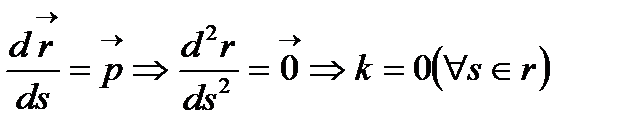
2) 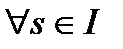
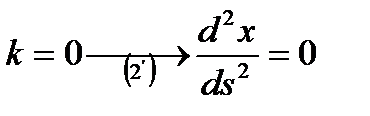 ,
, 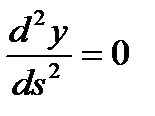 ,
, 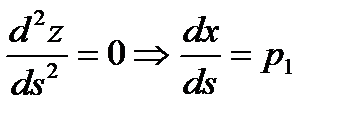 ,
, 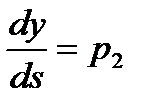 ,
, 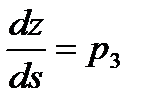 .
.
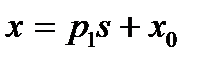 ,
, 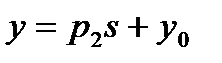 ,
, 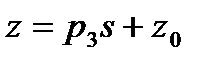 , ал бұдан
, ал бұдан 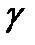 -
- 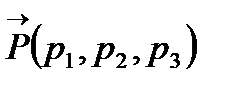 векторына параллель түзу не түзудің бөлігі, яғни
векторына параллель түзу не түзудің бөлігі, яғни 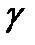 - қарапайым сызық.
- қарапайым сызық.
2. Сызықтың жылжымалы репері. 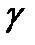 сызығының барлық нүктесіндегі қисықтығы нольден өзге делік. Онда оның әрбір нүктесінде
сызығының барлық нүктесіндегі қисықтығы нольден өзге делік. Онда оның әрбір нүктесінде 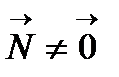 , сондықтан сызықтың әрбір нүктесінде
, сондықтан сызықтың әрбір нүктесінде 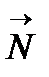 векторына параллель түзу өтеді.
векторына параллель түзу өтеді.
Анықтама: 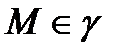 нүктесі арқылы өтетін,
нүктесі арқылы өтетін, 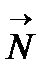 векторына параллель түзу бас нормаль деп аталады.
векторына параллель түзу бас нормаль деп аталады. 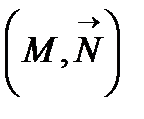 түрінде белгіленеді.
түрінде белгіленеді.
Лемманы осыдан 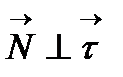 екені шығады. Сондықтан бас нормаль
екені шығады. Сондықтан бас нормаль 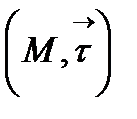 жанамасына перпендикуляр.
жанамасына перпендикуляр.
Анықтама: 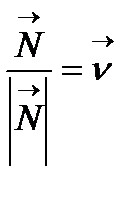 векторы бас нормальдың бірлік векторы деп аталады.
векторы бас нормальдың бірлік векторы деп аталады. 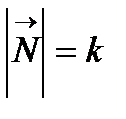 болғандықтан
болғандықтан 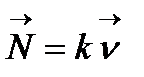 , ал бұдан
, ал бұдан 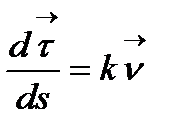 (3)
(3)
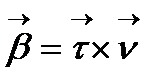 векторын қарастырайық.
векторын қарастырайық.
Анықтама: 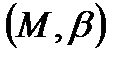 түзуі
түзуі 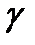 сызығының
сызығының 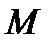 нүктесіндегі бинормаль деп аталады, ал
нүктесіндегі бинормаль деп аталады, ал 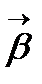 бинормальдың бірлік векторы деп аталады.
бинормальдың бірлік векторы деп аталады. 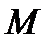 нүктесі,
нүктесі, 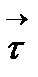 ,
, 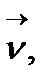
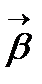 векторлар үштігі
векторлар үштігі 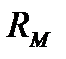 ортонормаланған реперін анықтайды. Бұл репер
ортонормаланған реперін анықтайды. Бұл репер 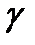 сызығының
сызығының 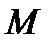 нүктесіндегі канондық репері деп аталады. Тегіс сызықтың қисықтығы нольге тең емес әрбір нүктесінде канондық репері бар. Осы
нүктесіндегі канондық репері деп аталады. Тегіс сызықтың қисықтығы нольге тең емес әрбір нүктесінде канондық репері бар. Осы 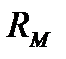 репердің координат жазықтықтары сәйкесінше төмендегіше аталады:
репердің координат жазықтықтары сәйкесінше төмендегіше аталады:
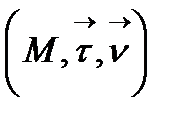 - жанасушы жазықтық
- жанасушы жазықтық
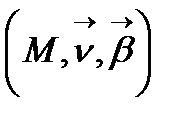 - нормаль жазықтық
- нормаль жазықтық
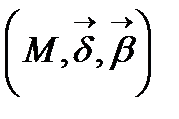 - түзетуші жазықтық.
- түзетуші жазықтық.
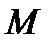 нүктесі
нүктесі 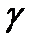 сызығының бойымен жылжығанда
сызығының бойымен жылжығанда 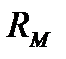 репері де өзгереді, сондықтан
репері де өзгереді, сондықтан 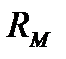 жылжымалы репер деп аталады.
жылжымалы репер деп аталады.
3. 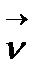 - бірлік вектор болғандықтан,
- бірлік вектор болғандықтан, 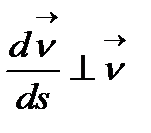 , бұдан
, бұдан 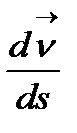 векторы түзетуші жазықтыққа параллель, сондықтан оны
векторы түзетуші жазықтыққа параллель, сондықтан оны 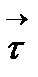 ,
, 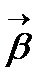 векторлары бойынша жіктеуге болады, яғни
векторлары бойынша жіктеуге болады, яғни
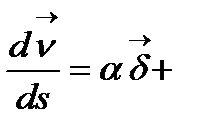 æ
æ 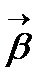 (4)
(4)
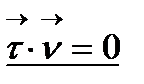 теңдігі дұрыс. Осы теңдікті S бойынша дифференциалдасақ:
теңдігі дұрыс. Осы теңдікті S бойынша дифференциалдасақ:
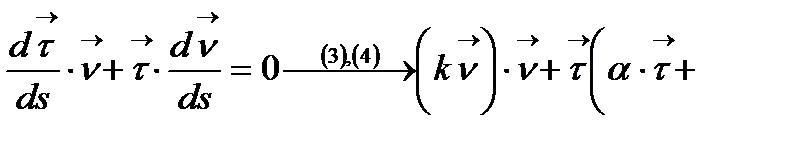 æ
æ 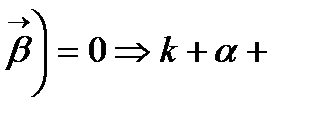 æ
æ 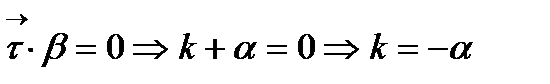 .
.
Онда (4) формула 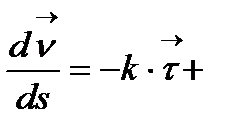 æ
æ 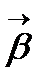 (5) түріне көшеді. Сонымен қатар
(5) түріне көшеді. Сонымен қатар 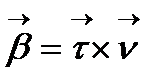 теңдеуі белгілі, оны s бойынша дифференциалдасақ:
теңдеуі белгілі, оны s бойынша дифференциалдасақ: 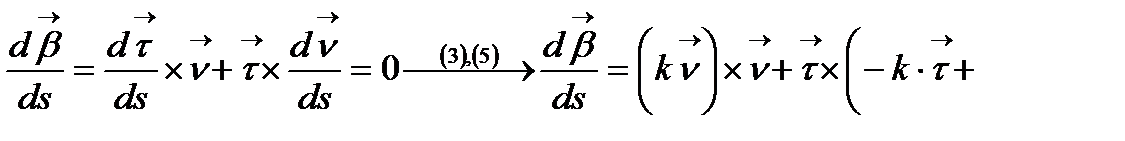 æ
æ 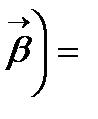 æ
æ 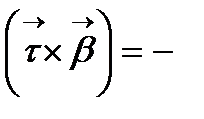 æ
æ 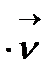 , сонымен
, сонымен 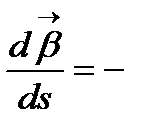 æ
æ 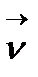
Мына формулаларды таптық:
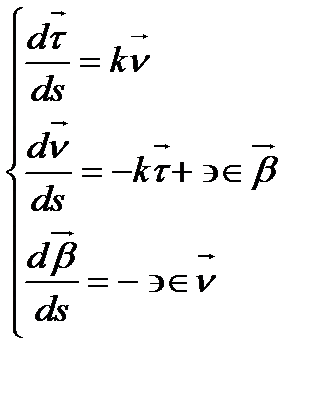 (6)
(6)
Бұл формулалар Френе формулалары деп аталады. Тегіс сызықтардың теориясы осы формулаларға негізделген.
4. Сызық бұралуы.
Анықтама. 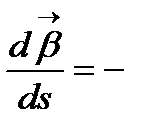 æ
æ 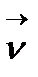 формуласындағы æ саны
формуласындағы æ саны 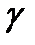 сызығының М нүктесіндегі бұралуы деп аталады.
сызығының М нүктесіндегі бұралуы деп аталады.
Сызықтың бұралуы S параметрлерінің функциясы болады. Табиғи параметрлермен сызықтың бұралуын есептейтін формуланы
Қорытып шығарайық.
I Френе формуласын 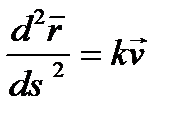 түрінде жазсақ,
түрінде жазсақ,
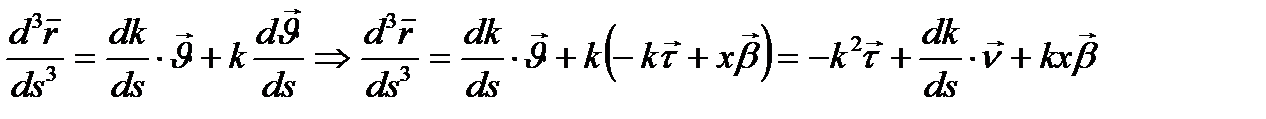
Мына аралас көбейтіндіні есептейік:
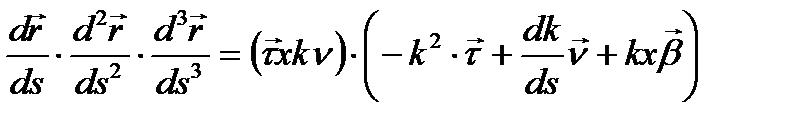
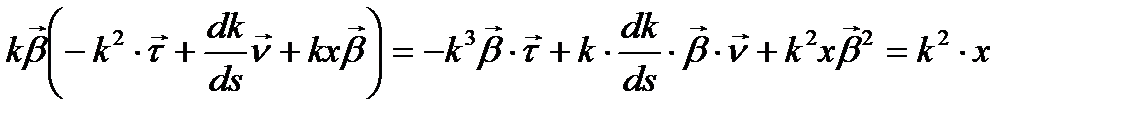
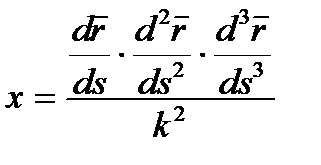 (7)
(7)
5. Жазық сызық.
Анықтама: Барлық нүктесі бір жазықтықта жататын сызық жазық (плоская линия) сызық деп аталады.
Жазық сызықтың қасиеттері:
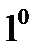 . Жазық сызықтың жанасушы жазықтығы сызық жатқан жазықтықпен беттеседі.
. Жазық сызықтың жанасушы жазықтығы сызық жатқан жазықтықпен беттеседі.
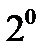 . Жазық сызықтың бас нормалі сызық жазықтығында жатады және бас нормальді сызықты нормалі деп атайды.
. Жазық сызықтың бас нормалі сызық жазықтығында жатады және бас нормальді сызықты нормалі деп атайды.
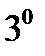 . Жазық сызықтың барлық нүктесіндегі бұралуы нольге тең болады.
. Жазық сызықтың барлық нүктесіндегі бұралуы нольге тең болады.
Теорема. Егер сызықтың барлық нүктесіндегі бұралуы нольге тең болса, мұндай сызық жазық сызық болады.
1) 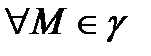
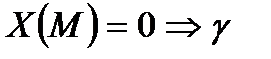 жазық сызық.
жазық сызық.
Д-уі: х=0 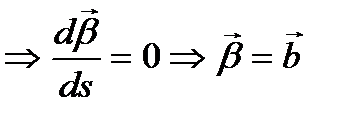 (тұрақты вектор), онда
(тұрақты вектор), онда 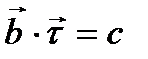 теңдігінен
теңдігінен 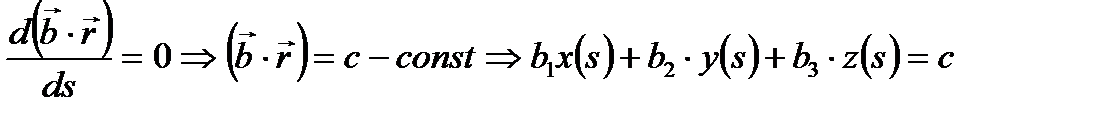 жазықтың теңдеуі. Мұнда
жазықтың теңдеуі. Мұнда 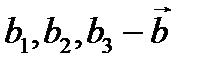 вектор координаты, ал бұдан
вектор координаты, ал бұдан 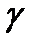 сызық бар нүктелері
сызық бар нүктелері 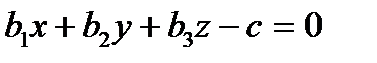 теңдеуімен берілген жазықтықта жататыны шығады, яғни
теңдеуімен берілген жазықтықта жататыны шығады, яғни 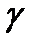 жазық сызық.
жазық сызық.
6. Сызықтың кез келген параметр жағдайында қисықтығы және бұралуын есептеу.
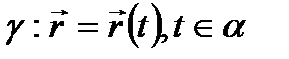 (8)
(8)
Сызықтың 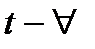 параметр болған жағдайда Канонд, қисықтығын, бұған есептеу формуласын табу керек.
параметр болған жағдайда Канонд, қисықтығын, бұған есептеу формуласын табу керек.
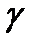 сызығында S табиғи параметрін енгіземіз және S=h(t) делік. (параметр алмастыру функциясы берілген) Егер
сызығында S табиғи параметрін енгіземіз және S=h(t) делік. (параметр алмастыру функциясы берілген) Егер 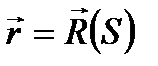
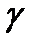 сызығының табиғи параметрленуі болса, онда
сызығының табиғи параметрленуі болса, онда 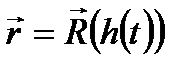 теңдеуі (1) теңдеумен бірдей болады, сондықтан
теңдеуі (1) теңдеумен бірдей болады, сондықтан
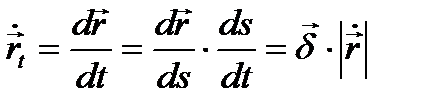 (2)
(2)
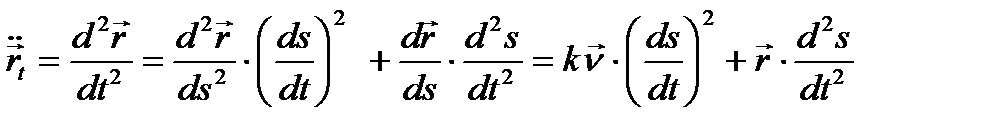 (3)
(3)
(3) теңдәктен 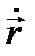 векторы жанасушы жазықтыққа параллель екені шығады.
векторы жанасушы жазықтыққа параллель екені шығады.
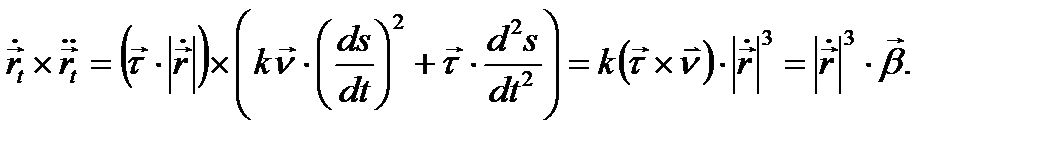 (*)
(*)
көбейтуді тапсақ
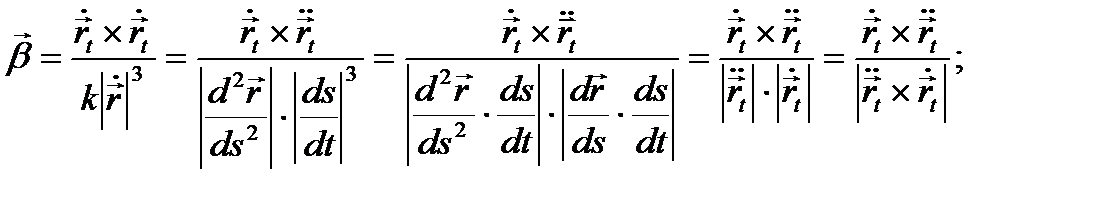
Сонымен 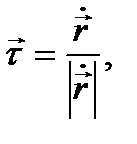
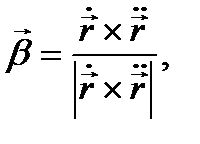
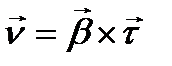
(*) 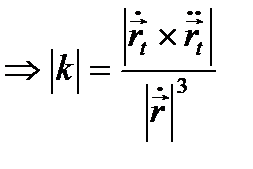 .
.
Енді Х-ң формуласын қорытып шығарайық, ол үшін 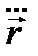 векторын табайық.
векторын табайық.
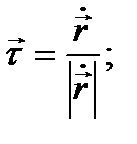
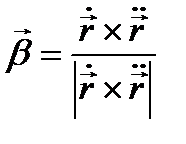
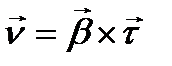
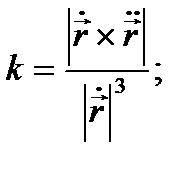
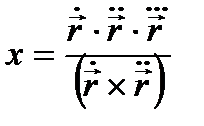 .
.
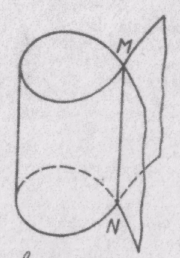
7. Винттік сызық.
Кеңістіктегі 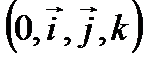 берілсін. Кеңістіктің М(х,у,z) нүктесі мына екі шартты қанағаттандыратынкүрделі қозғалыс жасайды:
берілсін. Кеңістіктің М(х,у,z) нүктесі мына екі шартты қанағаттандыратынкүрделі қозғалыс жасайды:
1) 0z осін бірқалыпты айналады.
2) 0z осіне параллель бірқалыпты орын ауыстырады.
Осылайша қозғалатын М нүктесінің t қозғалыс заңдылығын табу керек.
Айталық t уақыт жиелігін де бұл нүкте М(х,у,z) орнында болсын. P- М нүктесінің х0у ортогональ проекциясы болсын. P(х,у,о) М нүктесі 0z осін
айнала қозғалғанда P нүктесі хоу жазықтығында о нүктесін бірқалыпты айналады. Айталық М нүктесінің бастапқы жағдайы А(а,0,0) нүктесімен беттесіп P нүктесінің (а>0) айналуын бірқалыпты болғандықтан <А0р айналу бұрышы Қозғалыс уақыты t-ға пропорционал болады. Жеңілдік үшін пропорцияның к делік, яғни <А0р=t.
бұдан 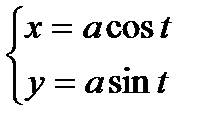 екенің көреміз.
екенің көреміз.
М нүктесі 0z осінің бағытында бірқалыпты орын ауыстыратын болғандықтан, ығысу аралығы t уақытқа пропорционал болады.
Z=b*t (b-const- біржақты ығысу) Сонымен М нүктесінің қозғалыс заңдылығы былайша болады:
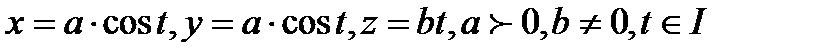
Бұл теңдеулер кеңістігінде кейбір элементар сызықты анықтайды.Және ол к винттік сызық деп аталады.
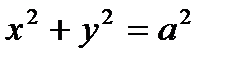 екенің ескеріп, винттік сызық дөңгелек цилиндрге жататының байқаймыз. Векторлық формуласы:
екенің ескеріп, винттік сызық дөңгелек цилиндрге жататының байқаймыз. Векторлық формуласы:
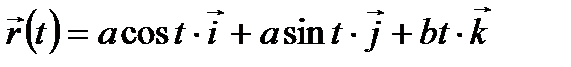 Винттік сызық үшін
Винттік сызық үшін 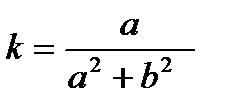
§1.Бет ұғымы.
1.1. Екі скаляр аргументтің вектор функциясы.
V - үш өлшемді векторлық кеңістік, G - екі өлшемді аралық (не R2; не 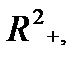 не квадрат
не квадрат 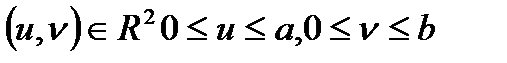 ) берілсін.
) берілсін.
Анықтама. Егер қандай да бір заңдылық бойынша 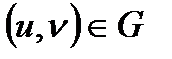
«нүктесіне» кейбір 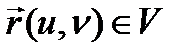 векторы сәйкес келсе, онда G аралығында екі аргументтің u, v вектор функциясы
векторы сәйкес келсе, онда G аралығында екі аргументтің u, v вектор функциясы 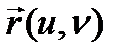 анықталған (берілген) делінеді, белгілеуі
анықталған (берілген) делінеді, белгілеуі 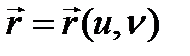
Анықтама. 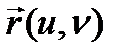 вектор функциясы
вектор функциясы 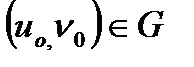 нүктесінің маңайында ақырсыз аз функция деп аталады, егер
нүктесінің маңайында ақырсыз аз функция деп аталады, егер 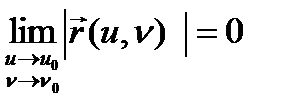 болса.
болса.
Анықтама. 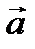 векторы
векторы 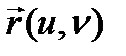 функциясының
функциясының 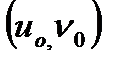 нүктесіндегі шегі деп аталады, егер
нүктесіндегі шегі деп аталады, егер 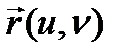 -
- 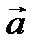 айырмасы осы нүктенің маңайында ақырсыз аз функция болса.
айырмасы осы нүктенің маңайында ақырсыз аз функция болса.
Анықтама. 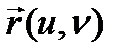 функциясы
функциясы 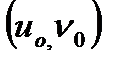 нүктесінде үздіксіз деп аталады, егер
нүктесінде үздіксіз деп аталады, егер 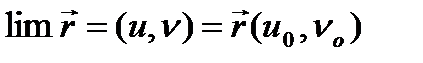
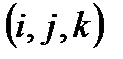 базисінде
базисінде 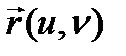 векторын G аралығының
векторын G аралығының
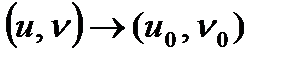
әрбір нүктесіндегі 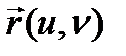
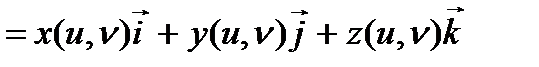
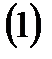 түрінде жіктесек,
түрінде жіктесек, 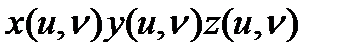 коэффициенттері G аралағында анықталған u,v айнымалыларының сан функциялары болады. Бұл функцияларды
коэффициенттері G аралағында анықталған u,v айнымалыларының сан функциялары болады. Бұл функцияларды 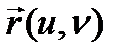 вектор функциясының
вектор функциясының 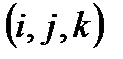 базисіндегі координаталары деп атайды. Егер
базисіндегі координаталары деп атайды. Егер 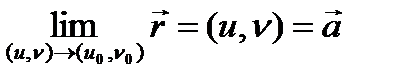 және
және 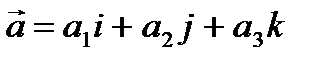 болса, онда
болса, онда 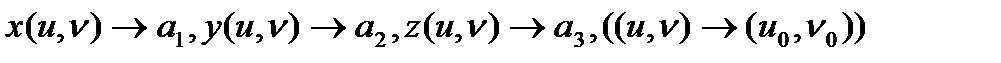 болады.
болады.
Анықтама. 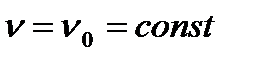 десек
десек 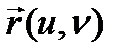 -бір аргументтің вектор функциясының аламыз, бұл фукция кейбір сан аралықта анықталады. Осы аралықтың кейбір нүктесінде
-бір аргументтің вектор функциясының аламыз, бұл фукция кейбір сан аралықта анықталады. Осы аралықтың кейбір нүктесінде 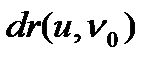 туындысы бар болса, онда
туындысы бар болса, онда 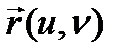 функциясының
функциясының 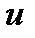 айнымалысы бойынша дербес туындысы деп атайды, былайша белгілеуі:
айнымалысы бойынша дербес туындысы деп атайды, былайша белгілеуі: 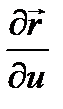 не
не 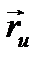 дәл осылайша
дәл осылайша 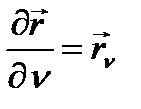 дербес туындысы анықталады.
дербес туындысы анықталады.
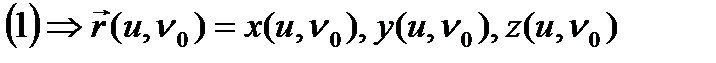
Сызықтар тақырыбындағы теорема 1 бойынша 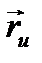 және
және 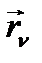 дербес туындылары табылады, сонда тек егер
дербес туындылары табылады, сонда тек егер 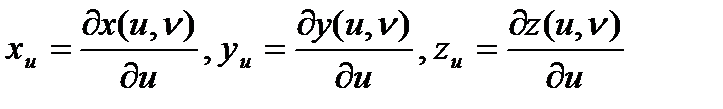 және
және 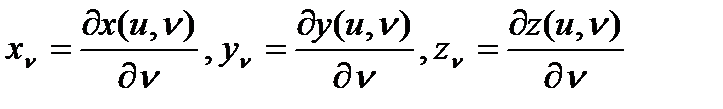 дербес туындылары бар болса. Осы теорема бойынша
дербес туындылары бар болса. Осы теорема бойынша
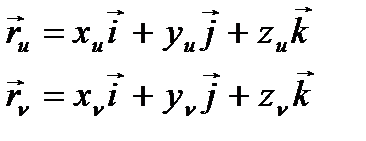
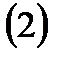
теңдіктері дұрыс болады.
Анықтама. 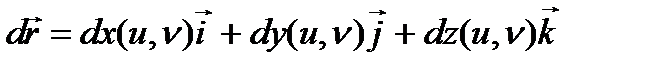
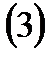
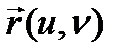 дифференцилды функциясы деп аталады.
дифференцилды функциясы деп аталады.
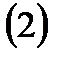 ,
, 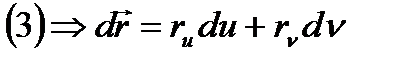
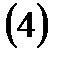
1.2 Бет ұғымына қатысты түсініктер. Беттің әртүрлі теңдеулері
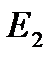 -евклид кеңістігінде жазықтығында тік бұрышты
-евклид кеңістігінде жазықтығында тік бұрышты 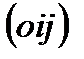 координаталар жүйесін қарастырып,
координаталар жүйесін қарастырып, 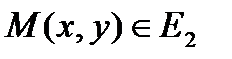 нүктесіне
нүктесіне 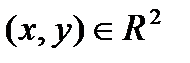 қосына сәйкесіке қойсақ,
қосына сәйкесіке қойсақ, 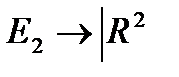 биективті бейнелеуді аламыз. Бейнелеу гомеоморфизм болады. Осыны ескерсек
биективті бейнелеуді аламыз. Бейнелеу гомеоморфизм болады. Осыны ескерсек 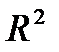 сандық кеңістіктегі
сандық кеңістіктегі 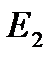 жазықтығымен;
жазықтығымен; 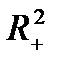 кеңістігін
кеңістігін 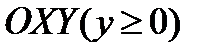 жарты жазықтығымен; сандық квадратты
жарты жазықтығымен; сандық квадратты 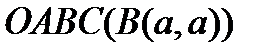 квадраттымен алмастыруға болады.
квадраттымен алмастыруға болады.
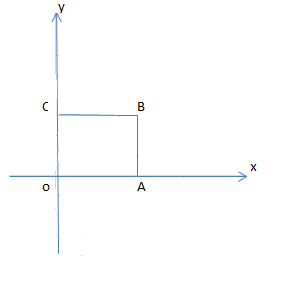 (1-сурет)
(1-сурет)
Анықтама. Жазықтықтық, жарты жазықтықтық, квадрат фигуралары қарапайым бет деп аталады.
Анықтама. Қарапайым беттердің біріне гомеоморфты фигураны элементар бет деп атайды. Мысалы: эллипстік параболоид, гиперболалық параболоид, жазықтыққа гомеоморфты фигуралар, яғни олар элементар беттер, жарты сферада элементар бет, себебі ол дөңгелекке гомеоморфты.
Анықтама. Бет деп, элементар беттердің шекті немесе есепті жиынымен бүркеуге болатын 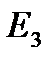 кеңістігіндегі фигураны айтады. Мысалы: сфера, эллипсоид, эллипстік цилиндр – беттер.
кеңістігіндегі фигураны айтады. Мысалы: сфера, эллипсоид, эллипстік цилиндр – беттер.
Анықтама. 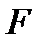 бетінің
бетінің 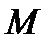 нүктесі кәдімгі нүкте деп аталады, егер оның
нүктесі кәдімгі нүкте деп аталады, егер оның 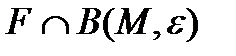 маңайы табылса.
маңайы табылса.
Кәдімгі нүкте ішкі және шекаралық болып бөлінеді. Егер 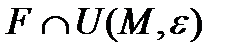 қимасы жазықтыққа гомеоморфты болса,
қимасы жазықтыққа гомеоморфты болса, 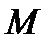 -ішкі нүкте болады, ал жарты жазықтыққа гомеоморфтті болса,онда
-ішкі нүкте болады, ал жарты жазықтыққа гомеоморфтті болса,онда 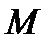 -шеакаралық нүкте болады.
-шеакаралық нүкте болады.
Анықтама. 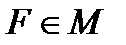 нүктесі кәдімгі нүкте емес болса, оны ерекше нүкте деп атайды.
нүктесі кәдімгі нүкте емес болса, оны ерекше нүкте деп атайды.
Анықтама. Әрбір нүктесі кәдімгі нүкте болатын бет жай бет деп аталады. Мысалы: эллипсоид, эллипстік цилиндр гиперболоидтар жай беттер. Конустық бет – жай бет емес, себебі төбесі ерекше нүкте.
 кәдімгі нүкте
кәдімгі нүкте
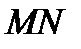 - түзу нүктелері ерекше нүктелер.
- түзу нүктелері ерекше нүктелер.
Беттің әртүрлі теңдеулері (параметрлік, векторлық теңдеулері, тік бұрышты координаттар берілген теңдеу)
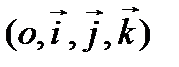 тік бұрышты координаталар жүйесі берілсін.
тік бұрышты координаталар жүйесі берілсін. 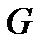 - екі өлшемді облыс,
- екі өлшемді облыс, 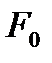 - элементар бет болсын.
- элементар бет болсын.
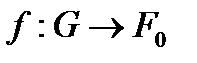 гомеоморфизмін қарастырайық. Осы гомеоморфты
гомеоморфизмін қарастырайық. Осы гомеоморфты 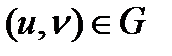 ʺнүктесіʺ
ʺнүктесіʺ 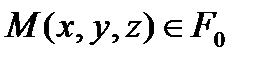 нүктесіне көшсе, онда
нүктесіне көшсе, онда 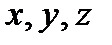 айнымалары
айнымалары 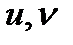 айнымаларының
айнымаларының 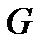 облысда анықталған функциялары болады, яғни
облысда анықталған функциялары болады, яғни
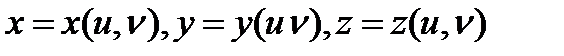
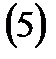
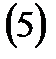 теңдеулер
теңдеулер 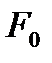 бетінің параметрлік теңдеулері деп аталады. Бұл теңдеулер
бетінің параметрлік теңдеулері деп аталады. Бұл теңдеулер
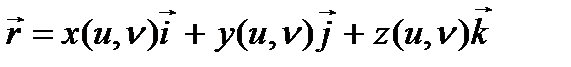
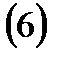
векторлық теңдеуімен мәндес, мұнда 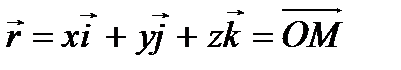
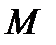 нүктесінің радиус –векторы.
нүктесінің радиус –векторы. 
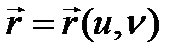
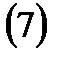 -
- 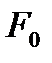 бетінің векторлық теңдеуі.
бетінің векторлық теңдеуі.
Кеңістікте 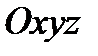 тік бұрышты декартық координат жүйесі берілсе
тік бұрышты декартық координат жүйесі берілсе 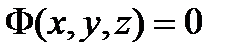
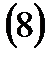 теңдеуі қандайда бір бетті анықтайды.
теңдеуі қандайда бір бетті анықтайды.
 2015-05-05
2015-05-05 1802
1802








