Тегіс беттер

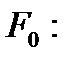
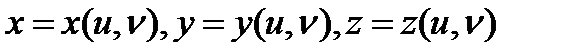
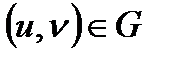
2.1. Тегіс беттің анықтамасы Айталық 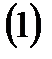элементар беті берілсін.

Анықтама. 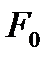элементар беті 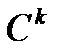класының 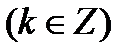тегіс беті деп аталады, егер теңдеулердң оң бөліктері 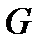облысында 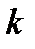ретті үздіксіз дербес туындылары бар функциялар және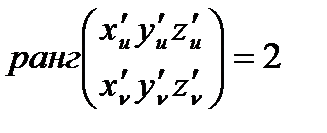 теңдігі орындалсын.

Анықтама. 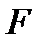жай беті 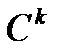класының тегіс бет деп аталады, егер оның әрбір 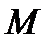нүктесінің 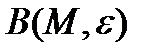маңайы табылып, 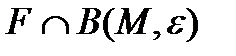қимасы 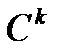класының элементар тегіс беті болатындай 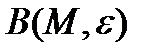маңайы табылса.

теңдеулер 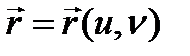векторлық теңдеулерімен мәндес. Жоғарыдағы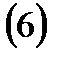

теңдеуден 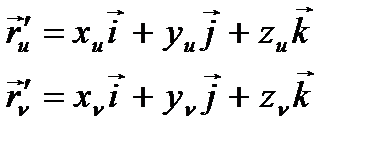теңдеулері шығады.

-шарты геометрия тұрғысынан алғанда 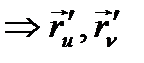- сызықтың тәуелсіз векторлар,ол болса

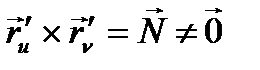
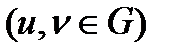
Бет бойындағы нүкенің қисық сызықты координаттары

Егер 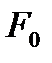элементар бетінің 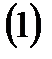теңдеулерінде 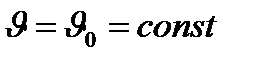болса, ал 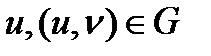шартын қанағаттандыратын өзгереді десек, бір аргументтің 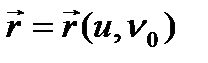функциясыны 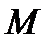нүктесінің 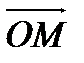радиус – векторы. 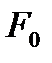бетінде бойында жатқан кейбір тегіс қисықты сызықты анықтайды.

Бұл сызықты 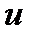сызығы деп атайды, және 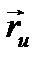векторы осы сызыққа 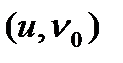нүктесіндегі жанаманың бағыттаушы векторы болады.

Дәл осылайша әрбір 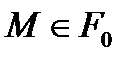нүктесі арқылы 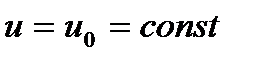болғанда сызығы өтеді, және векторы осы сызыққа 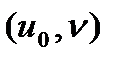нүктесіндегі жанаманың бағыттаушы векторы болады.

Қорытынды: Сонымен 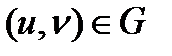болса, 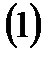теңдеулер бойынша анықталатын 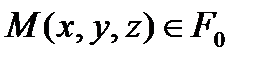нүктесі табылады, яғни 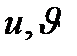параметрлері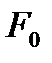

бетінің 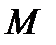нүктесін толық анықтайды. Осыны ескеріп 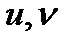параметрлері 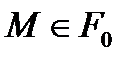нүктесінің қисық сызықты координаттары деп атайды.

Бұл қортынды 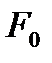бетінің кез келген 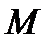нүктесі үшін дұрыс болады. Яғни әрбір 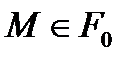нүктесі үшін 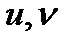сызықтары табылады. Осындай сызықтар тобының координатталық тор деп атайды.

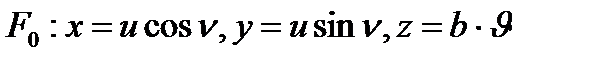
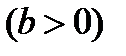
Мысал: теңдеулерімен берілген бет 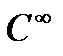класының тегіс бет екенін дәлелдеуге болады. Шынында, 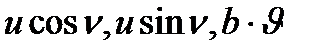функцияларын щексіз рет дифференциялдауға болады және

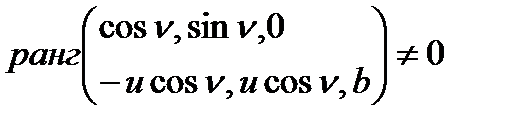
Бұл бет тік геликоид деп аталады.Тік геликоид осы кезде перпендикуляр тік бұрышпен қиятын түзудің кеңістікте төмендегідей күрделі қозғалысынан шығатын бет:

1) түзу осін бірқалыпты айналады.

2)түзу 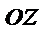осінің бағытында 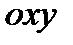жазықтығына параллелдігін сақтап жылжиды.

Беттің тегіс болу шарты.

а) Айталық 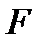беті 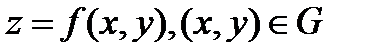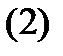теңдеулерімен берілсін.Қандай шарттар орындалғанда 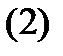теңдеу тегіс бетті анықтайды? Осыған жауап берейік.

Бұл теңдеуді 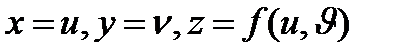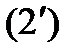параметрлік теңдеулерімен алмасуға болады. Анықтама бойынша 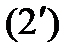теңдеулері 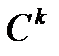класының тегіс бетін анықтау үшін олардың оң бөліктерінің бойынша ретті үздіксіз дербес туындылары бар болу қажетті және жеткілікті. Сонымен, 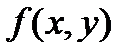функциясының (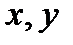) бойынша үздіксіз дербес туындылары бар болса, онда 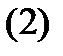теңдеу кеңістікте 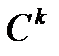класының тегіс бетін анықтайды.

б) Енді координаттылары 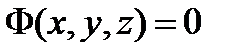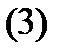теңдеулерін қанағаттандыратын кеңістік нүктелерінің 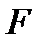жиыны қарастырайық. Қандай шарттар орындалғанда 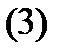теңдеуі тегіс бетті анықтайды? Бұл сұраққа төмендегі теорема жазап береді.

Теорема. 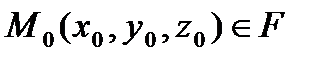нүктесінде екі шарт орындалады:

а) 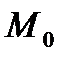нүктесінің кейбір 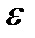маңайында 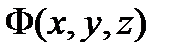функциясы және оның 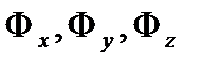дербес туындылары үздіксіз.

б) 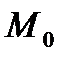нүктесінде 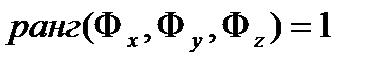болса, онда 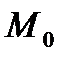нүктесінінің 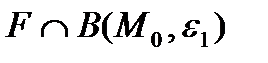қимасы 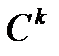класының тегіс беті болатындай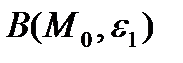 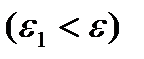маңайы табылады.

Мысал: 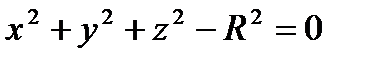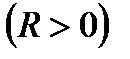сфера кез келген нүктесінде теореманың а), б) шарттары орындалады. Олай болса сфера класының тегіс беті болады.

§3. Жанама жазықтық және нормаль

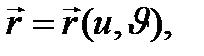
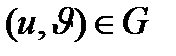
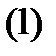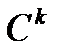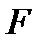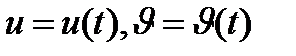
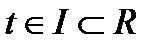
теңдеуімен класының тегіс беті берілсін және 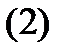болсын. Мұнда 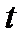айнымалы 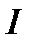аралығында өзгергенде 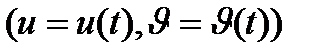жұбы обылысынан шықпайды. 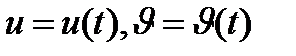функциялары 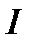арлығында үздіксіз 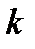ретті туындылары бар және 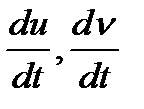туындылары нолден өзге болсын делік.

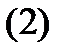теңдіктерден 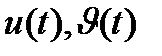өрнектерін 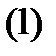теңдеуге қойсақ,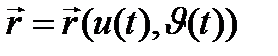 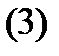теңдеуін аламыз. Бұл теңдеудің оң жағы 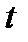скаляр аргументінен тәуелді функция, осы өрнекті 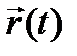десек,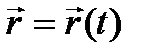 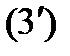теңдеуін аламыз.

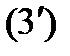теңдеуі 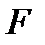бетінде жатқан 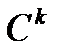класының тегіс сызығын анықтайды. Егер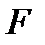 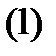теңдеумен берілген 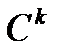класының тегіс беті болса, онда оның әрбір 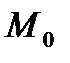нүктесі арқылы өтетін 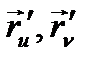векторлары осы нүкте арқылы өтетін жазықтыққа параллель болады. Осы жазықтықты 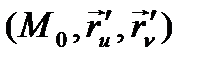түрінде белгілейік.

Теорема. Егер 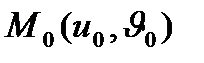нүктесі 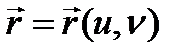теңдеуімен берілген 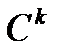класының 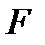тегіс бетінде жатса, онда осы нүктеде 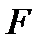бетінде жататын барлық тегіс сызықтарға жүргізілген жанамалар центрі 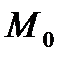нүктесі болатын түзулер шоғын құрайды және бұл түзулер шоғы 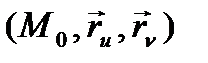жазықтығында жатады.

Анықтама. 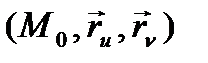жазықтығы 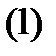теңдеумен берілген 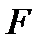бетіне 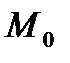нүктесіндегі жүргізілген жанама жазықтығы деп аталады.

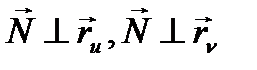болғанда 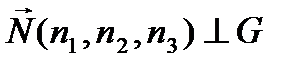болады. Олай болса, 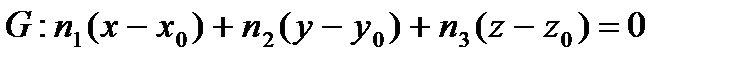жанама жазықтықтың теңдеуі болады.

Анықтама. тегіс бетіне 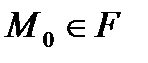нүктесінде жүргізілген нормаль деп, осы нүкте арқылы өтетін жанама жазықтыққа перпендикуляр түзуді айтады, оның теңдеуі.

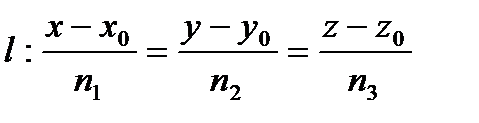түрінде болады.

Мысалы:

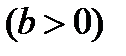
тік геликоидына 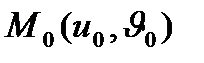нүктесінде жүргізілген жанама жазықтықтың теңдеуі жазу керек.

Лемма. 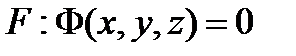жабық теңдеулері берілсін, онда 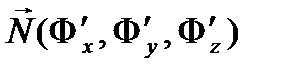векторы осы бетке 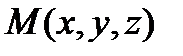нүктесінде жүргізілген жанама жазықтыққа перпендикуляр вектор болады.

§4 Беттің бірінші квадрат формасы, оның қолдануы

4.1 Бірінші квадрат форманың анықтамасы

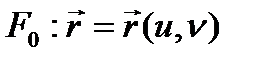
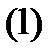тегіс беті берілсін.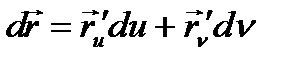 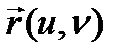- функция толық дифференциалы. Осы теңдікті квадраттайық

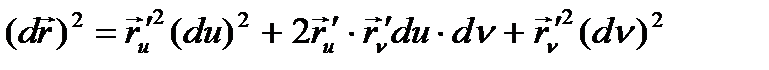
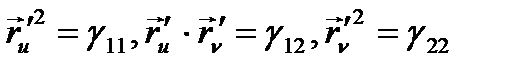
десек

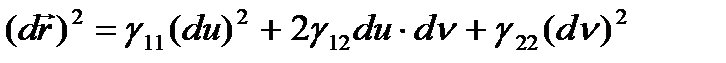
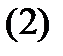теңдігін аламыз.

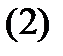теңдіктің оң жағындаңы өрнек 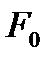бетінің I квадрат формасы немесе сызықтық элементі деп аталады.

Ескерту. 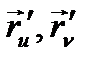функциялары 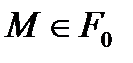нүктесін қисық сызықты координаттары болатын 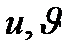айнымалыларының вектор функциялары болғандықтан, 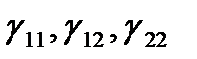координаттарында осы айнымалыларының функциялары болады.

4.2. Бірінші квадрат форманың қолданылуы

а) Бет бойындағы сызық доғасының ұзындығы.

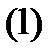теңдеумен берілген 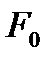тегіс бетінде жатқан 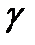- тегіс сызығы қарастырыйық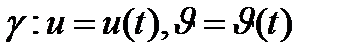

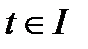
Осы 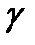сызығы кеңістікте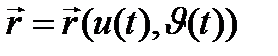 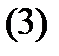теңдеуімен беріледі:

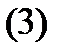теңдеуі 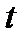бойынша дифференциал

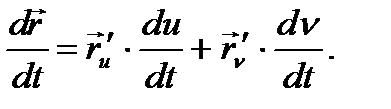
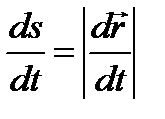теңдігін және теңдігін ескерсек, доғасының ұзындығы,

мұнда сызығын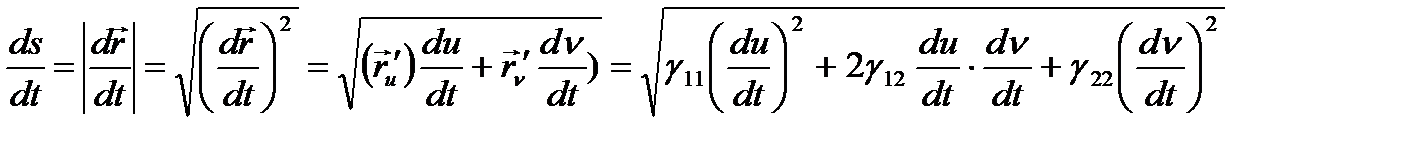

теңдігін аламыз, яғни

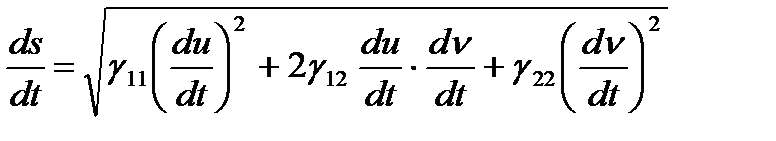
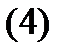
теңдігі дұрыс болады.

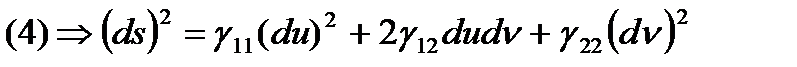
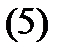бұл теңдіктен беттің I квадрат формасының мәні осы бетте жатқан сызықтың нүктесі осы сызық бойымен жылжығанда шығатын доғаның ұзындығы дифференциалының квадраты болатынын көреміз. 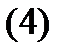теңдіктен 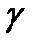сызықтың ұштары 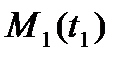және 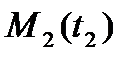нүктелері болатын доғасының ұзындығын есептейтін формуланы аламыз.

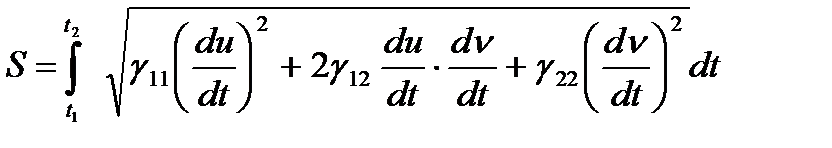
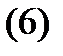- доғаның ұзындығының формуласы.

б) Бет бойындғы екі сызықтың арасындағы бұрыш.

Айталық 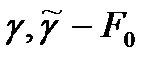бетінде жатқан, 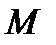нүктесі арқылы өтетін сызықтар болсын.

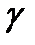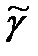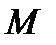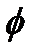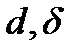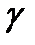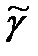Анықтама. және сызықтарының арасындағы бұрыш деп, оларға нүктесінде жүргізілген жанамалардың арасындағы бұрышты айтады. Оны делік - әріптерімен және сызықтары бойында диффенциалдау символын белгілейік 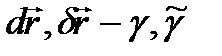сызықтарына нүктесінде жүргізілген жанамалардың бағыттаушы векторлары болады. Олай болса,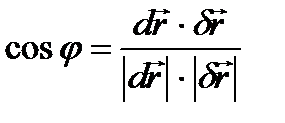

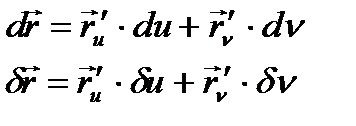екенін ескерік,

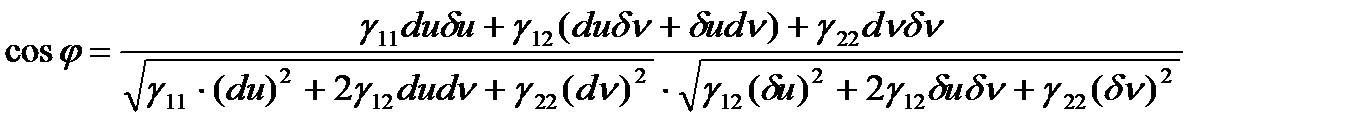
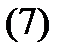- екі сызықтың арасындағы бұрыш.

в) Тегіс беттің бөлігін ауданы

Математикалық анализ курсында осы шарттарды қанағаттандыратын бет үшін аудан ұғымы енгізгеді және ауданның формуласы қортып шығаралады. Ауданы табылатын бет квадратталатын бет деп аталады.

Квадратталған- беттің қарапайым мысалы.

1) 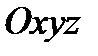жүйесінде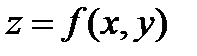 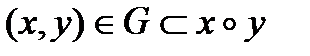теңдеуімен берілген бет.

Мұндай 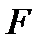бетінің ауданы 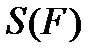мына формуламен өрнектеледі

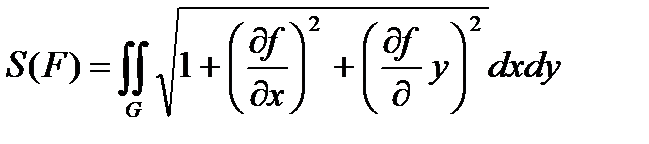
2)

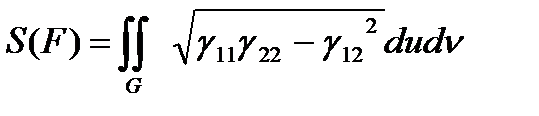
3) 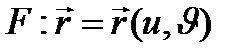беті берілсе, оның әрбір нүктесінде

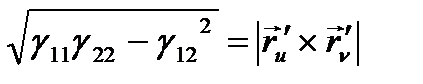
теңдігі орындалатынын көрсетуге болады. Шынында да, егер 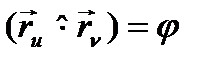десек, онда 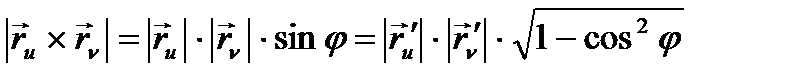бұдан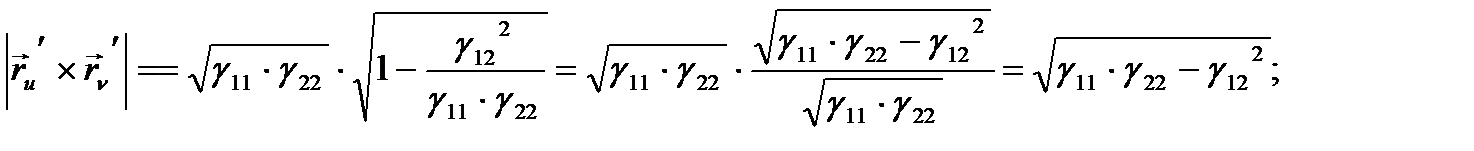

Олай болса

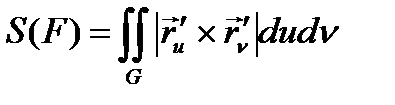
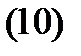
1- Мысал. 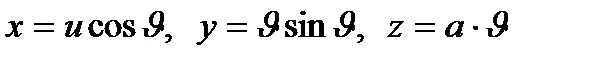тік геликоидтың І квадрат формасын табыңыз.

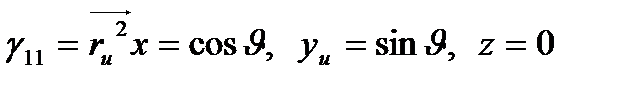
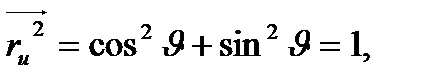
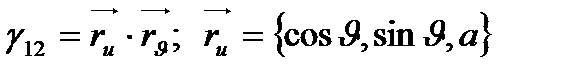
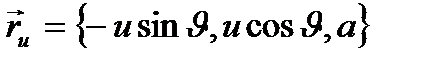
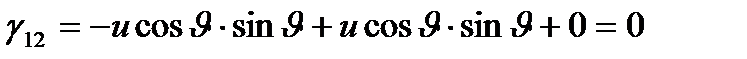
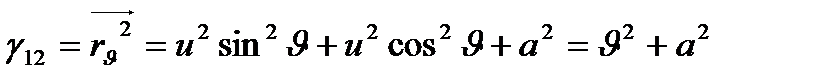
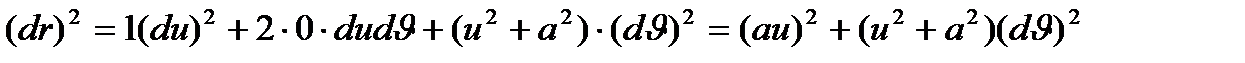
2–мысал. І квадарат формасы 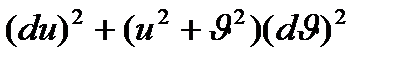түрінде болатын бет бойында жатқан 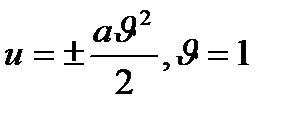қисық сызықты үшбұрыштың периметрі және ішкі бұрыштарын табыңыз:

Шешуі:

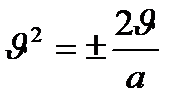
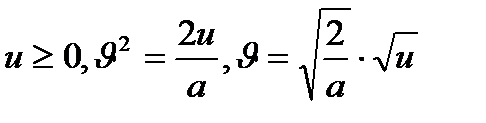
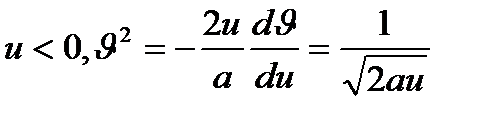
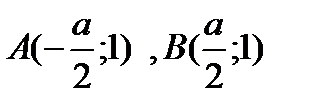
А

В

V

U

a/2

a/2

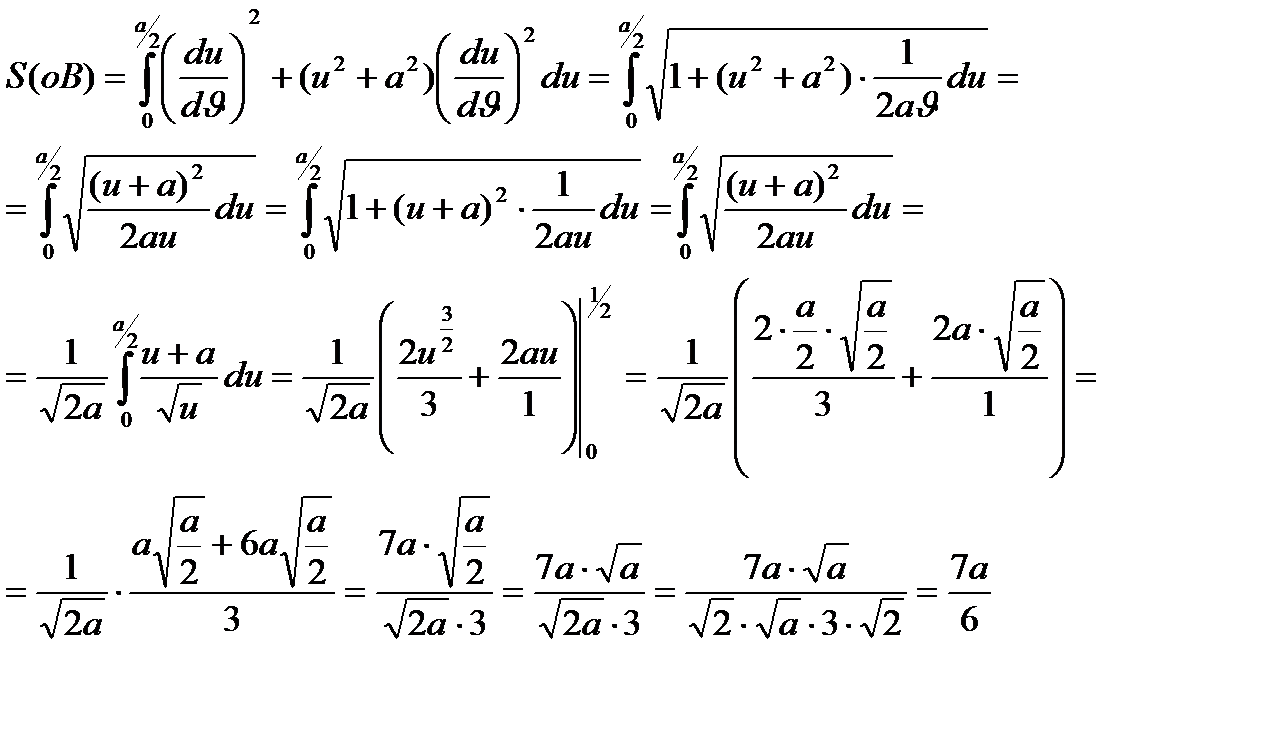
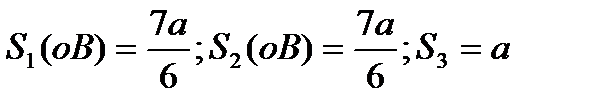
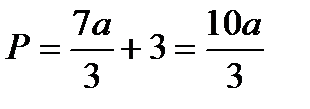
3–есеп. Бірінші квадрат формасы 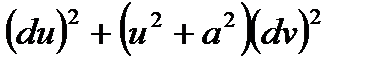түрінде болатын беттің бойында жатқан 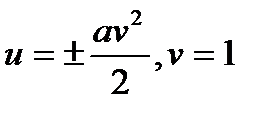қисық сызықты үшбұрышының ішкі бұрыштарын табыңыз.

Шешуі: 2 – суреттегідей. , ,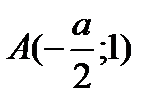

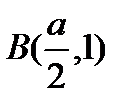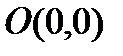
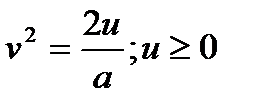болса, .

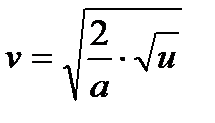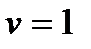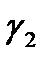сызығы үшін , сызығы үшін 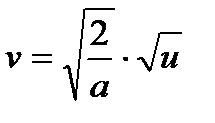болғандықтан , .

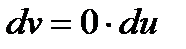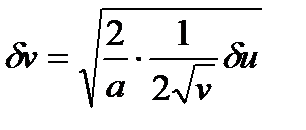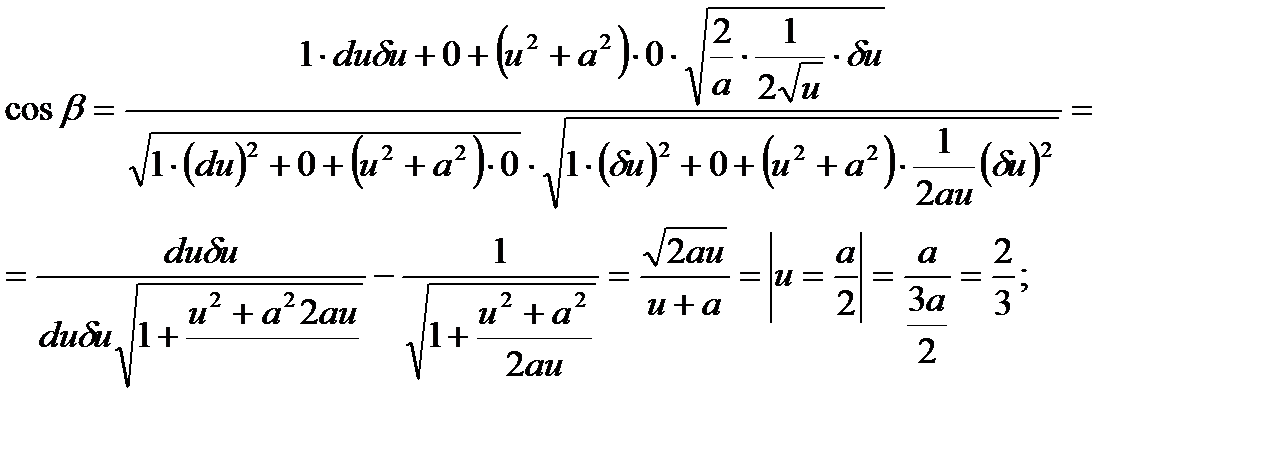
Сол сияқты 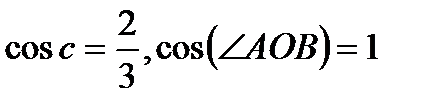болады

. Беттің II квадраттық формасы. Беттегі қисықтың қисықтығы. Беттің II квадраттық формасы, қолданылуы.

.

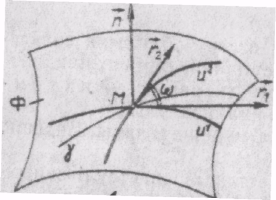
1.Айталық, Ф беті 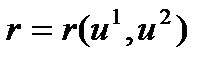,теңдеуімен берілген Ск 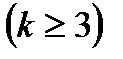класының тегіс элементар беті және 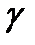осы беттегі тегіс сызық болсын (2-сурет). М нүктесі 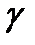қисығы бойынша жылжығанда мынаны шығарып аламыз:

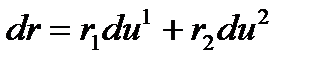
қысқаша 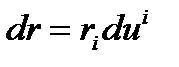(13)

М нүктесіндегі Ф бетіне 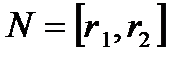нормаль векторының нормасын табайық:

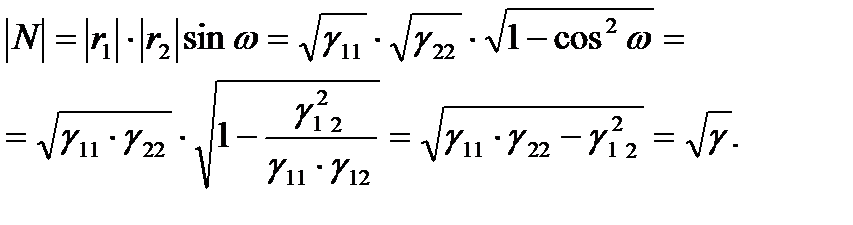
Мұндағы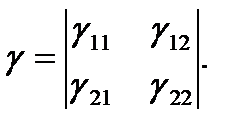

Нормальдық бірлік векторы мынадай: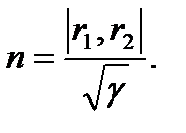

(13) өрнегін пайдаланып, мынаны табамыз:

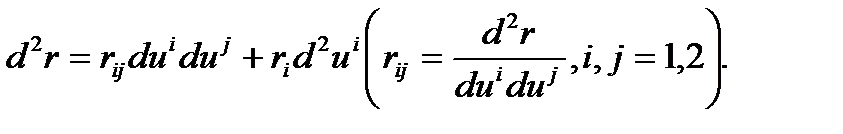
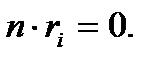n┴ri болғандықтан, Сондықтан да

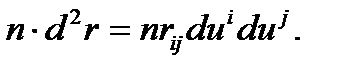(14)

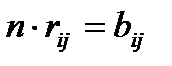деп белгілейік. Демек,

2 сурет

Сонда (14) теңдік мына түрге келеді:

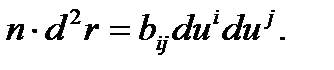(15)

Бұл теңдіктің оң жақ бөлігі Тм векторлық кеңістігінде анықталған квадраттық форма болады. Мұны 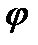арқылы белгілейік:

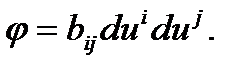
(15) формуланың көрсетуіндей, 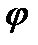формасының мәні М нүктесі ( 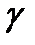қисығының бойымен жылжыған кездегі) радиус-векторының екінші дифференциалының сол бетке М нүктесінен жүргізілетін n бірлік нормаль векторға түсетін ортогональ проекциясы болып табылады. Бұл 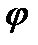формасы беттің екінші квадраттық формасы деп аталады.

2. М нүктесінде 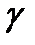сызығына жүргізілген жанаманың бірлік векторы:

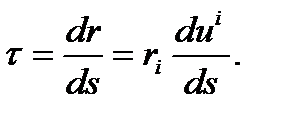
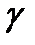сызығының M нүктесіндегі иілім векторын табайық: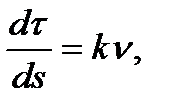

яғни 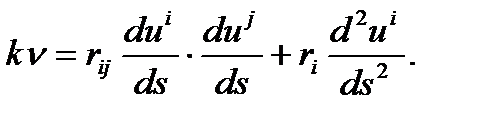(16)

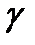қисығының М нүктесіндегі kn нормаль қисықтығы деп бетке жүргізілген нормальдық n бірлік векторына проекциясын айтамыз:

kn=npn(kv)=n·(kv). (17)

Олай болса,

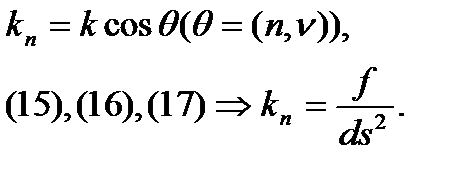
(13) теңдіктен Т(М) жазықтығында 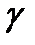сызығына жүргізілген (МТ) жанамасының, бағыты du1:du2 қатынасы бойынша анықталады деген қорытындыға келеміз. (19) формула М нүктесінен өтетін қисықтың нормаль қисықтығы тек жанаманың бағытына байланысты екендігін көрсетеді. Олай болса, беттегі М нүктесі аркылы өтетін және осы нүктеде ортақ (МТ) жана-масы бар барлық тегіс қисықтардың М нүктесінде бір, тек қана бір нормаль қисықтығы болады.

3. М 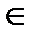Ф нуктесінен Т(М) жазықтығындағы әрбір бағытта ұзындығы 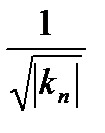болатын кесінділерді өлшеп саламыз, мұңдағы ku - осы бағытта М нүктесі арқылы бетте жүргізілген түзулердің нормаль қисықтығы. Осы кесінділердің екінші ұштарынан пайда болған фигура М нүктесіндегі бет қисықтығының индикатрисасы (немесе Дюпен индикатрисасы) деп аталады. Ол қандай фигура болады?

Т(М) жанама жазықтығында 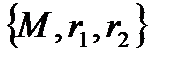аффиндік координаталар системасын енгізейік. Айталык, Р(x,y) - индикатрисасының ақпа координаталары болсын. Сонда

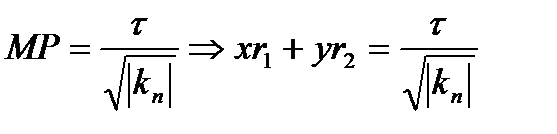(τ-МР векторының орты).

Бұл теңдікті квадрат дәрежеге шығарып және du1:du2=х:у екенін ескерсек, мынаны табамыз:

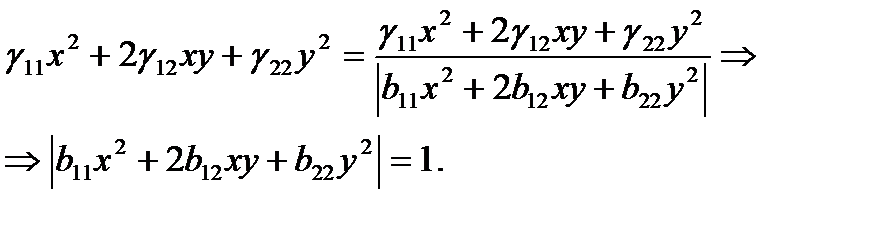
Ол Дюпен индикатрисасының тендеуі болып табылады. Демек, былай болады:

а) эллипс егер 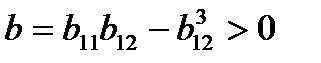(мұнда М нүктесі эллипстік нүкте деп аталады) болса;

б) түйіндес гиперболалар пары, егер b<0 (М нүктесі - гиперболалық нүкте) болса;

в) параллель түзулер пары, егер b=0 (М нүктесі - параболалық нүкте) болса.