2015-05-05
9475Ариант B-24
Условие задания.
Пользуясь критерием устойчивости Михайлова, Найквиста определить устойчивость одноконтурной системы управления, имеющую в разомкнутом состоянии передаточную функцию вида
W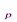 
(s) =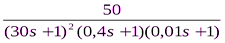 
,
Построить годографы Михайлова и Найквиста. Определить частоту среза системы.
Определить критическое значение коэффициента усиления системы.
Решение.
- Построение годографа Михайлова.
А) Выписываем характеристический полином для замкнутой системы
A(s) = 50 + (30s+1)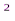 
(0,4s+1)(0,01s+1) = 50+(900 
+60s+1)(0,004 +0,41s+1) = 3,6 
+369,24 
+924,604 
+60,41s+51.
Б) Преобразуем к виду s→ ωj
A(s) = 3,6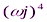 
+369,24 
+924,604 
+60,41 
+51 = 3,6ω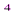 
-369,24jω 
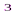-924,604ω 
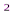+60,41jω+51
В) Выделим действительную и мнимую часть.
A= U(
)+jV(), где U() – действительная часть, а V(
) – мнимая часть.
U() = 3,6ω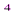 
-924,604ω 
+51
V() = ω(60,41-369,24 ω )
Г) Построим годограф Михайлова:
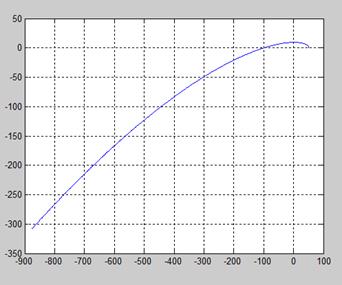
Рис.1. Годограф Михайлова при ω = 0:000,1:0,1.
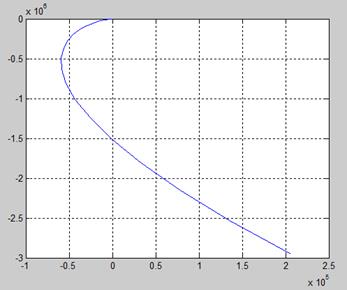
Рис.2. Годограф Михайлова при ω = 0:1:20.
Д) Проверим устойчивость системы с помощью критерия Михайлова:
Критерий Михайлова: Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.1 и рис.2), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ∞ n квадрантов, где n - степень характеристического полинома.
Из решения видно (см. рис.1 и рис.2), что годограф удовлетворяет всем условиям критерия:
- Начинается на положительной вещественной полуоси при w = 0
- Обходит в положительном направлении все 4 квадранта (степень полинома n=4) при ω
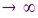. - Делаем вывод, что данная разомкнутая система устойчива.
- Построение годографа Найквиста.
А) Произведем замену в АФЧХ s→ ωj
W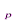 
(s) =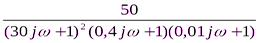 
,
Б) Раскроем скобки и выделим действительную и мнимую часть в знаменателе
W (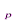
) = 
,
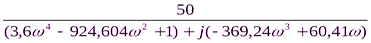В) Умножим на сопряженное и выделим действительную и мнимую часть
,
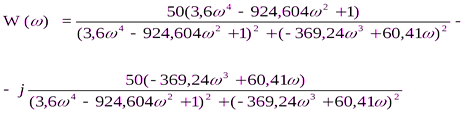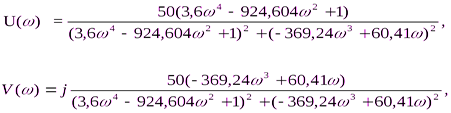
где U() – действительная часть, а V() – мнимая часть.
Г) Построим годограф Найквиста:
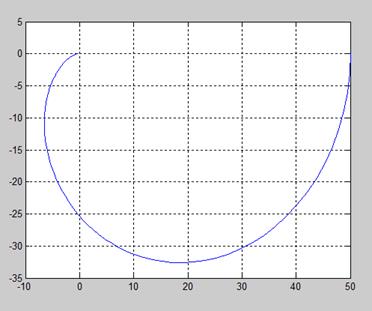
Рис.3. Годограф Найквиста.
Д) Проверим устойчивость системы с помощью критерия Найквиста:
Критерий Найквиста: Для того чтобы система, которая в разомкнутом состоянии была устойчива, была устойчива и в замкнутом, необходимо, чтобы годограф Найквиста при изменении частоты от нуля до бесконечности не охватывал точку с координатами (-1; j0).
Из решения видно (см. рис.3), что годограф удовлетворяет всем условиям критерия:
- Годограф меняет свое направление по часовой стрелке
- Годографом не охватывается точка (-1; j0)
- Делаем вывод, что данная разомкнутая система устойчива.
- Определение критического значения коэффициента усиления системы.
А) В пункте 2 уже были выделены действительная и мнимая части
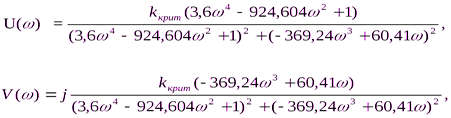
Б) Для того, чтобы найти критическое значение коэффициента усиления системы необходимо приравнять мнимую часть к нулю, а действительную к -1
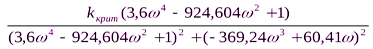= -1 (1)
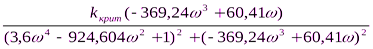= 0 (2)
В) Найдем из второго (2) уравнения
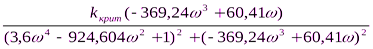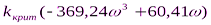= 0
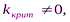
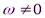
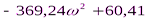= 0
= 0
, 
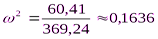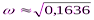
В) Подставляем в первое (1) уравнение и находим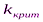 
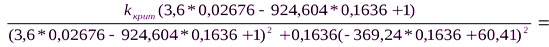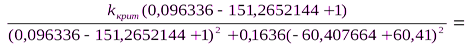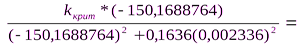-1
-1
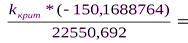-1
-1
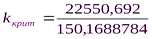
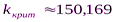- критическое значение коэффициента усиления системы.
- Определение частоты среза системы.
А) Приведем основные формулы
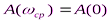
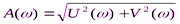, где U(
) и V() – действительная и мнимая части соответственно.
Б) Подставляем в формулу имеющиеся данные и находим частоту среза системы
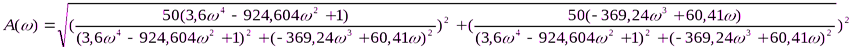
A(0) = 50/51
В) Найдем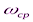 
(при помощи Wolfram Alpha):
((50*(3.6*w^4-924.6*w^2+1)/((3.6*w^4-924.6*w^2+1)^2+(-369.24*w^3+60.41*w)^2))^2+(50*(-369.24*w^3+60.41*w)/((3.6*w^4-924.6*w^2+1)^2+(-369.24*w^3+60.41*w)^2))^2)^1/2 = 50/51
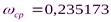- частота среза системы.
Литература:
1.Методы классической и современной теории автоматического управления. Том 1.
Анализ и статистическая динамика систем автоматического управления. М: Изд. МГТУ им Баумана. 2000 г.
2. Воронов А.А. Теория автоматического управления. Т. 1-3, М., Наука, 1992
Скачать работу
