Если диссипация энергии в системе отсутствует, в ней не может быть равновесия.
Флуктуационно-диссипационная теорема
Теория равновесных флуктуаций, представленная выше, нашла свое завершение в виде флуктуационно-диссипационной теоремы (ФДТ), сформулированной в 1951—1952 гг.
Физическое содержание этой теоремы заключается в следующем.
Рассмотрим замкнутую систему, находящуюся в равновесном состоянии. Пусть, в результате флуктуации, какая-то часть системы – ее подсистема – была выведена из положения равновесия. Очевидно, что для этого подсистема должна получить дополнительную энергию от остальной части системы за счет их взаимодействия. Поскольку вся система замкнута, при возвращении подсистемы в положение равновесия она должна отдать эту энергию обратно. Это возможно только при наличии процессов диссипации (трения) в системе.
Следовательно, статистическое равновесие предполагает наличие диссипации. Например, маятник, выведенный толчком из положения равновесия, может вернуться в исходное неподвижное состояние только при наличии трения.
Количество энергии, возвращаемое подсистемой, пропорционально коэффициенту трения (диссипации) и зависит от динамических свойств подсистемы. Поскольку вся система в целом изолирована и ее полная энергия остается постоянной, то, следовательно, количество энергии, получаемое подсистемой при флуктуации так же должно быть пропорционально коэффициенту диссипации в подсистеме.
Таким образом, ФДТ связывает интенсивность тепловых флуктуаций (точнее спектральную плотность мощности) подсистемы с коэффициентом диссипации и динамическими свойствами этой подсистемы.
 Электроны, находясь в проводящей среде, испытывают со стороны этой среды беспорядочные толчки, как и броуновская частица. Под действием этих толчков они совершают такое же беспорядочное движение. Чем интенсивнее эти толчки, тем более беспорядочным становится движение электрона, тем труднее электрону двигаться в направлении, задаваемым внешним электрическим полем, и тем больше тогда электрическое сопротивление среды. Поскольку электроны обладают зарядом, то, даже в отсутствие внешнего электрического поля, это беспорядочное движение приводит к появлению хаотического тока, среднее значение которого, естественно, равно нулю. Однако дисперсия этого тока и его спектральная плотность отличны от нуля.
Электроны, находясь в проводящей среде, испытывают со стороны этой среды беспорядочные толчки, как и броуновская частица. Под действием этих толчков они совершают такое же беспорядочное движение. Чем интенсивнее эти толчки, тем более беспорядочным становится движение электрона, тем труднее электрону двигаться в направлении, задаваемым внешним электрическим полем, и тем больше тогда электрическое сопротивление среды. Поскольку электроны обладают зарядом, то, даже в отсутствие внешнего электрического поля, это беспорядочное движение приводит к появлению хаотического тока, среднее значение которого, естественно, равно нулю. Однако дисперсия этого тока и его спектральная плотность отличны от нуля.
Найквист, анализируя это движение в резисторе с сопротивлением R, в 1927 году получил выражение для спектральной плотности мощности хаотического напряжения, возникающего на концах разомкнутого резистора в следующем виде: 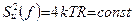 . Если резистор замкнуть, то в его цепи возникнет беспорядочный ток. Спектральная плотность мощности этого тока имеет следующий вид:
. Если резистор замкнуть, то в его цепи возникнет беспорядочный ток. Спектральная плотность мощности этого тока имеет следующий вид: 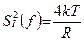 .
.
Замечание. При отсутствии реактивных элементов в цепи (емкости или индуктивности) спектральная плотность теплового шума остается постоянной вплоть до частот порядка 1012 Гц. Флуктуации с постоянным (однородным) шумовым спектром часто называют “ белым шумом ”.
Приведенные формулы получили название формул Найквиста. Впервые тепловые шумы измерил в 1927 году Джонсон. Этот вид шумов был предсказан Эйнштейном именно на основании анализа броуновского движения электронов.
Зная спектральную плотность напряжения или тока, можно найти их среднеквадратические значения в полосе частот D f = f 2– f 1: 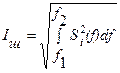 ,
, 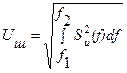 .
.
Поскольку спектральная плотность в формуле Найквиста постоянна, то 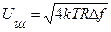 и
и 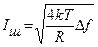 . Эти формулы также называют формулами Найквиста.
. Эти формулы также называют формулами Найквиста.
Проведем численную оценку результата измерения напряжения на разомкнутом резисторе. Пусть R= 1МОм, Т= 3000Си D f = 100Гц. Поскольку k= 1,38×10-23Дж/K, найдем U ш» 1,3×мкВ. Это – вполне заметная величина.
Легко видеть, что, измеряя шумовое напряжение, можно определить и температуру резистора. На этом принципе в настоящее время создано целое направление в измерительной технике – шумовая термометрия. Отметим, что совсем недавно американские ученые создали прибор для измерения сверхнизких температур с рекордной точностью, на основе измерения тепловых шумов тока, проходящего через контакт двух металлов.
 2014-02-13
2014-02-13 3182
3182








