Основные методы нахождения ранга матрицы

Используя элементарные преобразования, ранг матрицы можно вычислить одним из следующих способов.

1. Метод единиц и нулей. С помощью элементарных преобразований любую матрицу можно привести к такому виду, когда каждый ее столбец (строка) будет состоять только из нулей или нулей и одной единицы. В этом случае число единиц определяет ранг исходной матрицы.

2. С помощью элементарных преобразований исходную матрицу можно свести к треугольной. Если при этом на главной (побочной) диагонали полученной матрицы нет нулевых элементов, то ее определитель отличен от нуля.

3. Метод окаймляющих миноров. Минор M 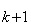порядка k + 1, содержащий минор M 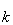порядка k, называется окаймляющим минор M 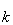. Если у матрицы А существует минор M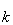 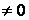, а все окаймляющие его миноры M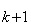 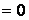, тоr(A) 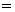k.

9) Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

Упорядоченный набор значений 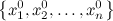называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

СЛАУ называется совместной, если она имеет, хотя бы одно решение.

В противном случае система называется несовместной.

Система называется определённой, если она совместна и имеет единственное решение.

В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.

Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

Система называется квадратной, если количество уравнений равно количеству неизвестных.

Определение. Переменная x_i называется свободной, если эта переменная не является разрешенной, а вся система уравнений — является разрешенной.